У виразі  (крок 11)
(крок 11)  нарощується, якщо
нарощується, якщо  не є простим. Але, разом з тим, треба враховувати обмеження
не є простим. Але, разом з тим, треба враховувати обмеження  .
.
У кроці 12 можливість  блокується переходом на побудову нового значення
блокується переходом на побудову нового значення  . Покажемо, що випадок
. Покажемо, що випадок  неможливий.
неможливий.
Позначимо у виразі  +
+  (крок 9) перший доданок через
(крок 9) перший доданок через  , а другий доданок - через
, а другий доданок - через  . Оцінемо розмір числа
. Оцінемо розмір числа  . Якщо число
. Якщо число  не є цілим, то
не є цілим, то  =
=  . Поділимо
. Поділимо  на
на 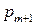 з остачею. Це можна записати як
з остачею. Це можна записати як  , де
, де  та
та  - цілі,
- цілі,  .
.
Тоді 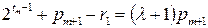 . Але
. Але  , звідки
, звідки  , тобто,
, тобто,
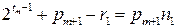 .
.
Оскільки, разом з тим,  , а
, а  за побудовою, то
за побудовою, то  .
.
Крім того,  . Останнє потрібно, щоб врахувати присвоювання
. Останнє потрібно, щоб врахувати присвоювання  у п. 9.
у п. 9.
Таким чином, двійковий запис числа  має вигляд
має вигляд  і містить серію нулів довжини, що практично дорівнює
і містить серію нулів довжини, що практично дорівнює  .
.
Аналогічно, для оцінки розміру числа 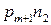 запишемо
запишемо  , де
, де  та
та  - цілі,
- цілі,  . Оскільки
. Оскільки  , то
, то 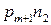
 . Кількість двійкових розрядів числа
. Кількість двійкових розрядів числа 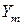 дорівнює
дорівнює  . Якщо всі вони - одиниці, то відповідне значення
. Якщо всі вони - одиниці, то відповідне значення  є максимальним, тобто завжди
є максимальним, тобто завжди  . Тому
. Тому 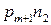
 , звідки:
, звідки:  .
.
Очевидно, для виразу  з п.11, для великого діапазону
з п.11, для великого діапазону 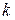 отримаємо
отримаємо  , оскільки
, оскільки  .
.
З цього випливає, що при додаванні чисел  одиниця переносу зі старшого розяду суми виникне дуже рідко.
одиниця переносу зі старшого розяду суми виникне дуже рідко.
Таким чином, вихід числа  на розрядність
на розрядність 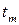 блокується у кроці 12 безпосередньою перевіркою, а чисел, що проходять перевірку, тобто мають розрядність
блокується у кроці 12 безпосередньою перевіркою, а чисел, що проходять перевірку, тобто мають розрядність 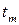 , достатньо багато.
, достатньо багато.
Тепер обгрунтуємо перевірку простоти числа  .
.
Перепозначимо  , де
, де  .
.
За теоремою Димитко, виконання умов кроку 13 достатньо для доведення простоти числа  , якщо
, якщо  . Покажемо, що ця умова виконується.
. Покажемо, що ця умова виконується.
Дійсно, якщо це не так, то  , звідки:
, звідки:  і
і 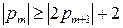 . За кроком 12 алгоритма,
. За кроком 12 алгоритма,  , до того ж,
, до того ж,  , де
, де  . Тоді
. Тоді  =
=  , тобто, залежно від
, тобто, залежно від 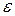 ,
,  , або
, або  , що є протиріччям.
, що є протиріччям.
На завершення приведемо процедуру С для побудови числа  порядку
порядку  за модулем
за модулем  - основи відкритого ключа цифрового підпису:
- основи відкритого ключа цифрового підпису:  .
.
1. Вибрати псевдовипадково число  :
:  .
.
2. Обчислити  .
.
3. Якщо  , перейти на крок 1, інакше,
, перейти на крок 1, інакше,  . Кінець процедури.
. Кінець процедури.
Лекции по синтаксису сложного предложения.

 (крок 11)
(крок 11)  нарощується, якщо
нарощується, якщо  не є простим. Але, разом з тим, треба враховувати обмеження
не є простим. Але, разом з тим, треба враховувати обмеження  .
. блокується переходом на побудову нового значення
блокується переходом на побудову нового значення  неможливий.
неможливий. +
+  (крок 9) перший доданок через
(крок 9) перший доданок через  , а другий доданок - через
, а другий доданок - через  . Оцінемо розмір числа
. Оцінемо розмір числа  . Якщо число
. Якщо число  не є цілим, то
не є цілим, то  =
=  . Поділимо
. Поділимо  на
на 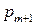 з остачею. Це можна записати як
з остачею. Це можна записати як  , де
, де  та
та  - цілі,
- цілі,  .
.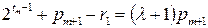 . Але
. Але  , звідки
, звідки  , тобто,
, тобто,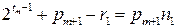 .
. , а
, а  за побудовою, то
за побудовою, то  .
. . Останнє потрібно, щоб врахувати присвоювання
. Останнє потрібно, щоб врахувати присвоювання  у п. 9.
у п. 9. і містить серію нулів довжини, що практично дорівнює
і містить серію нулів довжини, що практично дорівнює  .
.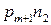 запишемо
запишемо  , де
, де  та
та  - цілі,
- цілі,  . Оскільки
. Оскільки  , то
, то  . Кількість двійкових розрядів числа
. Кількість двійкових розрядів числа 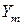 дорівнює
дорівнює  . Якщо всі вони - одиниці, то відповідне значення
. Якщо всі вони - одиниці, то відповідне значення  є максимальним, тобто завжди
є максимальним, тобто завжди  . Тому
. Тому  , звідки:
, звідки:  .
. з п.11, для великого діапазону
з п.11, для великого діапазону 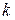 отримаємо
отримаємо  , оскільки
, оскільки  .
. одиниця переносу зі старшого розяду суми виникне дуже рідко.
одиниця переносу зі старшого розяду суми виникне дуже рідко.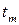 блокується у кроці 12 безпосередньою перевіркою, а чисел, що проходять перевірку, тобто мають розрядність
блокується у кроці 12 безпосередньою перевіркою, а чисел, що проходять перевірку, тобто мають розрядність  , де
, де  .
. . Покажемо, що ця умова виконується.
. Покажемо, що ця умова виконується. , звідки:
, звідки:  і
і 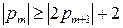 . За кроком 12 алгоритма,
. За кроком 12 алгоритма,  , де
, де  . Тоді
. Тоді  =
=  , тобто, залежно від
, тобто, залежно від 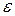 ,
,  , або
, або  , що є протиріччям.
, що є протиріччям. порядку
порядку  за модулем
за модулем  - основи відкритого ключа цифрового підпису:
- основи відкритого ключа цифрового підпису:  .
. :
:  .
. .
. , перейти на крок 1, інакше,
, перейти на крок 1, інакше,  . Кінець процедури.
. Кінець процедури.


