Формы представления уравнений
Обыкновенное дифференциальное уравнение n- го порядка можно записать в виде соотношения:
Уравнение включает независимую переменную x, а также неизвестную функцию y (x) и ее производные. Порядок уравнения определяется порядком старшей производной, входящей в уравнение. В дифференциальное уравнение могут входить также дополнительные переменные: m ,…, m k. В этом случае говорят, что неизвестная функция зависит от переменных m ,…, m k как от параметров. Наряду с уравнениями для одной неизвестной функции в теории дифференциальных уравнений рассматриваются системы уравнений. Система уравнений первого порядка, разрешенных относительно производных
называется нормальной системой. Введя векторные функции Y т=(y 1,…, yn), F т=(f 1,…, fn) можно записать систему (5) в векторной форме
Уравнение n -го порядка, разрешенное относительно старшей производной, имеет вид:
Уравнение n -го порядка легко свести к нормальной системе. Для этого введем обозначения:
Получим в результате систему уравнений первого порядка для неизвестных Пример 1.5. Нормальная система для частного случая уравнения колебаний Будем полагать независимую переменную действительной величиной. Неизвестные функции могут быть как действительными, так и комплексными функциями действительной переменной. Очевидно, что, если в уравнении первого порядка неизвестная функция является комплексной: y (x) = Re(y) +j Im(y), – то такое уравнение эквивалентно системе обыкновенных дифференциальных уравнений для действительных функций Re(y)и Im(y). Пример 1.6. Частное решение уравнения колебаний
|

 . (1.4)
. (1.4) (1.5)
(1.5)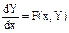 .
.
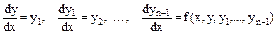 .
.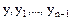 .
. имеет вид:
имеет вид:  .
. , где для краткости обозначено
, где для краткости обозначено  . Для проверки достаточно подставить выражения для
. Для проверки достаточно подставить выражения для  в исходное уравнение. С помощью такой же проверки легко убедиться, что действительная и мнимая части функции V:
в исходное уравнение. С помощью такой же проверки легко убедиться, что действительная и мнимая части функции V:  , – также являются решениями уравнения.
, – также являются решениями уравнения.


