Формы представления решения дифференциального уравнения
Решением системы дифференциальных уравнений
называется любая совокупность функций yi (x) (i =1,…, n), которые при подстановке в уравнения обращают их в тождества. Как правило, если дифференциальное уравнение разрешимо, то оно обладает бесчисленным множеством решений. Процесс нахождения решений называется интегрированием дифференциального уравнения. Если решение задано соотношением, определяющим y как неявную функцию x, то такое решение называется интегралом дифференциального уравнения. Для дифференциального уравнения первого порядка
интеграл может быть записан в виде:
где С – произвольная постоянная. При каждом фиксированном значении С выражение (1.8) определяет некоторое частное решение у=у (х) исходногоуравнения (1.7) как неявную функцию переменного х. Если С рассматривать как параметр, то выражение (1.8) определяет семейство решений у = у(х,С). Если выражение (1.8), в котором С рассматривается как параметр, определяет все множество решений соответствующего дифференциального уравнения, то это выражение называется общим интегралом данного дифференциального уравнения, а полученное из него выражение у = у (х, С) называется общим решением дифференциального уравнения. Обычно рассматриваются уравнений с правыми частями, непрерывными в некоторой области D изменения неизвестных функций у, и независимой переменной х. Очевидно, что при этом решения yi (x) представляют собой непрерывно дифференцируемые функции. Однако в приложениях иногда приходится иметь дело с уравнениями, правые части которых имеют разрывы (например, при описании ударных нагрузок, мгновенно приложенных сил и т. д.), поэтому и сами решения будут иметь разрывы производных. Тогда естественно в качестве решения системы уравнений рассматривать непрерывные функции yi (x) скусочно-непрерывными производными. При подстановке в уравнения они дифференцируются всюду, за исключением точек разрыва (или отсутствия) производных. Такое решение естественно назвать обобщенным решением.
|

 (1.6)
(1.6)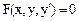 (1.7)
(1.7)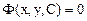 , (1.8)
, (1.8)


