Геометрическая интерпретация решения дифференциального уравнения
Решение Y(x)системы из n уравнений Для уравнения n-го порядка Пример 1.7. Частным решением уравнения колебаний
в случае малого коэффициента затухания a<<1 является функция Решение уравнения колебаний иллюстрируется рисунками 1.3 – 5. Значение коэффициента затухания выбрано равным
В простейшем случае одного уравнения
функция f (x, у)определяет поле направлений в заданной области D плоскости (х,у). Это поле направлений в каждой точке области D задается вектором t (x, у)сугловым коэффициентом f (x, у) (tg(a)= f (x, у)). В поле направлений можно выделить бесконечное множество интегральных кривых – бесконечное множество решений. На рисунках 1.6 и 1.7 приведены примеры полей направлений. Рисунки представляют собой активные вставки, созданные программой Mathcad. Для активизации вставок достаточно дважды щелкнуть мышкой в поле вставок. Активизация вставок позволяет изменять условия задачи; например, изменив знак На рисунке 1.6 показано поле направлений для уравнения
Показана также интегральная кривая, проходящая через точку (0,1). На рисунке 1.7 показаны поля направлений для уравнений
Для первого из этих уравнений угловой коэффициент поля направлений в каждой точке кроме точки (0,0) равен угловому коэффициенту прямой, направленной из начала координат в эту точку. Очевидно, что интегральными кривыми являются прямые, проходящие через начало координат. В этом легко убедиться, найдя решение уравнения. Перепишем уравнение в виде
Проинтегрируем уравнение, обозначив постоянную интегрирования
При построении второго графика заметим, что угловые коэффициенты поля напраправлений для первого и второго уравнений удовлетворяют условию ортогональности:
Следовательно, поле направлений для второго дифференциального уравнения ортогонально полю, показанному на левом графике. Для построения нового графика достаточно увеличить аргументы векторов поля на p/2. Поле направлений для второго уравнения показано на правом графике. Интегральными кривыми в данном случае являются окружности с центром в начале координат. В этом легко убедиться, проинтегрировав уравнение:
Здесь С – произвольная постоянная.
|

 можно интерпретировать геометрически как кривую в (n+1)-мерном пространстве переменных х,y1,...,yn, которая называется интегральной кривой. Подпространство переменных y1,..., ynназывается фазовым пространством, а проекция интегральной кривой на фазовое пространство– фазовой траекторией.
можно интерпретировать геометрически как кривую в (n+1)-мерном пространстве переменных х,y1,...,yn, которая называется интегральной кривой. Подпространство переменных y1,..., ynназывается фазовым пространством, а проекция интегральной кривой на фазовое пространство– фазовой траекторией. соответствующим (n+1)-мерным пространством является пространство переменных
соответствующим (n+1)-мерным пространством является пространство переменных  ; фазовым пространством является пространство переменных
; фазовым пространством является пространство переменных  .
.
 , где
, где  . Данное решение соответствует начальным условиям:
. Данное решение соответствует начальным условиям:  . При a=0 решение описывает колебания постоянной амплитуды с периодом, равным 2p. Если коэффициент затухания a>0, решение описывает затухающий процесс: амплитуда колебаний монотонно стремится к нулю.
. При a=0 решение описывает колебания постоянной амплитуды с периодом, равным 2p. Если коэффициент затухания a>0, решение описывает затухающий процесс: амплитуда колебаний монотонно стремится к нулю. . На рис. 1.3 показана зависимость V(t) – проекция интегральной кривой на плоскость V’(t)=0. Интегральная кривая в пространстве переменных
. На рис. 1.3 показана зависимость V(t) – проекция интегральной кривой на плоскость V’(t)=0. Интегральная кривая в пространстве переменных  показана на рис. 1.4. Кривая представляет собой спираль, “навитую” на ось t. Фазовая траектория показана на рис. 1.5.
показана на рис. 1.4. Кривая представляет собой спираль, “навитую” на ось t. Фазовая траектория показана на рис. 1.5.
 Пусть правые части уравнений нормальной системы (1.5) заданы в некоторой области D. Уравнения системы определяют в каждой точке этой области некоторое направление, задаваемое вектором t=(1, f 1, …, fn). Такая область пространства с заданным в каждой точке направлением называется полем направлений. Интегрирование системы уравнений геометрически интерпретируется как нахождение кривых, у которых направление касательной в каждой точке совпадает с направлением t, заданным в данном поле направлений.
Пусть правые части уравнений нормальной системы (1.5) заданы в некоторой области D. Уравнения системы определяют в каждой точке этой области некоторое направление, задаваемое вектором t=(1, f 1, …, fn). Такая область пространства с заданным в каждой точке направлением называется полем направлений. Интегрирование системы уравнений геометрически интерпретируется как нахождение кривых, у которых направление касательной в каждой точке совпадает с направлением t, заданным в данном поле направлений. (1.9)
(1.9) на рис. 1.6, построим поле направлений для затухающих экспонент. Для возвращения в Word достаточно щелкнуть мышкой вне поля вставки.
на рис. 1.6, построим поле направлений для затухающих экспонент. Для возвращения в Word достаточно щелкнуть мышкой вне поля вставки.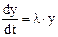 .
. и
и  .
. .
.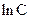 :
: .
.
 . Поле направлений показано на левом графике.
. Поле направлений показано на левом графике. .
.



