Плоские электромагнитные волны и их свойства. Английский физик Джеймс Клерк Максвелл в 1864 г
Английский физик Джеймс Клерк Максвелл в 1864 г. впервые получил уравнения, описывающие динамику новой формы материи – электромагнитного поля. Теория электромагнитного поля Максвелла основана на следующих положениях. 1. Всякое изменение магнитного поля создает в окружающем пространстве вихревое электрическое поле (рис. 1.1 а). Линии напряженности вихревого электрического поля расположены в плоскости, перпендикулярной линиям индукции переменного магнитного поля, и охватывают их; они образуют с вектором
2. Всякое изменение электрического поля возбуждает в окружающем пространстве вихревое магнитное поле, линии индукции которого расположены в плоскости, перпендикулярной линиям напряженности переменного электрического поля, и охватывают их (рис. 1.1 б). Линии индукции возникающего магнитного поля образуют с вектором Переменные электрическое и магнитное поля могут существовать в пространстве в отрыве от зарядов и токов проводимости как единое электромагнитное поле. В природе электрические и магнитные явления выступают как две стороны единого процесса. Деление электромагнитного поля на электрическое и магнитное зависит от выбора системы отсчета. Действительно, вокруг зарядов, покоящихся в одной системе отсчета, существует только электрическое поле; однако эти же заряды будут двигаться относительно другой системы отсчета и порождать в этой системе отсчета, кроме электрического, еще и магнитное поле. Таким образом, теория Максвелла связала воедино электрические и магнитные явления. Если возбудить с помощью колеблющихся зарядов переменное электрическое или магнитное поле, то в окружающем пространстве возникает последовательность взаимных превращений электрических и магнитных полей, распространяющихся от точки к точке. Максвелл показал, что скорость электромагнитных волн в вакууме
где e0 и m0 – электрическая и магнитная постоянные, e0 = 8,85 · 10–12 Ф/м, m0 = 4p · 107 Гн/м. Эта скорость совпадает со скоростью света в вакууме. На этом основании Максвелл выдвинул смелое предположение, что световая волна – это лишь разновидность электромагнитных волн. Основные свойства электромагнитных волн, распространяющихся в пустом пространстве, можно получить, исходя из фундаментальных законов электромагнитной теории Максвелла. Наибольшей простотой отличаются плоские монохроматические волны. Плоская монохроматическая волна – это идеализация. Несмотря на ограниченную применимость такой идеализированной модели, она во многих случаях полезна для описания реальных волн. В плоских монохроматических волнах зависимость векторов
Волновой вектор Непосредственно из теории Максвелла следует: 1. Векторы 2. Векторы 3. В электромагнитной волне модули векторов Пусть плоская электромагнитная волна распространяется в положительном направлении оси z, вектор Уравнение этой волны запишется так:
На рис. 1.3 дан «моментальный снимок» такой волны. Из рисунка видно, что колебания электрического вектора Если направление распространения волны изменится на противоположное, то уравнение волны примет вид:
«Моментальный снимок» такой волны приведен на рис. 1.4. Расстояние между двумя ближайшими точками, колеблющимися в одинаковых фазах, есть длина волны l. Полеты управляемых космических аппаратов на далекие расстояния к планетам Солнечной системы продемонстрировали, что скорость распространения электромагнитных волн велика, но не бесконечна; она составляет 300 000 км/с. Например, команды, передаваемые в виде радиоволн космическим аппаратам, находящимся на Луне, приходят туда с запаздыванием по времени примерно на 1 с. Мы выяснили, что в электромагнитной волне колеблются две векторные величины:
|

 «левый винт» (их направление соответствует правилу Ленца).
«левый винт» (их направление соответствует правилу Ленца).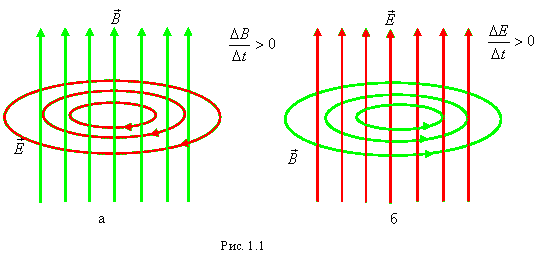
 «правый винт».
«правый винт».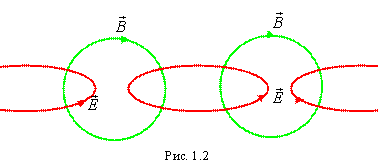 Оба эти поля являются вихревыми, причем векторы
Оба эти поля являются вихревыми, причем векторы 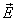 и
и 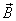 расположены во взаимно перпендикулярных плоскостях. Процесс распространения электромагнитного поля схематически показан на рис. 1.2. Этот процесс, являющийся периодическим во времени и пространстве, представляет собой электромагнитную волну.
расположены во взаимно перпендикулярных плоскостях. Процесс распространения электромагнитного поля схематически показан на рис. 1.2. Этот процесс, являющийся периодическим во времени и пространстве, представляет собой электромагнитную волну.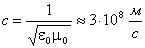 ,
, .
.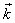 определяет направление распространения поверхности постоянной фазы (волновой поверхности). Его модуль
определяет направление распространения поверхности постоянной фазы (волновой поверхности). Его модуль 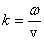 , где
, где  – фазовая скорость волны.
– фазовая скорость волны.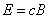 . Это соотношение выполняется в любой точке пространства в любой момент времени.
. Это соотношение выполняется в любой точке пространства в любой момент времени.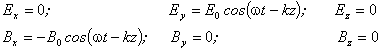 .
.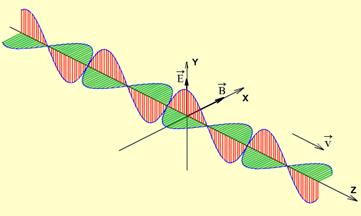 Рис. 1.3
Рис. 1.3
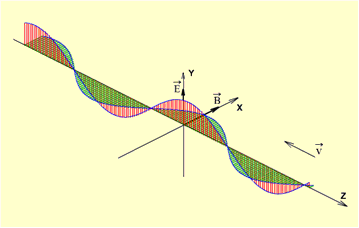 Рис. 1.4
Рис. 1.4
 . В фиксированной точке пространства векторы
. В фиксированной точке пространства векторы 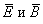 изменяются со временем по гармоническому закону, причем эти изменения происходят в одной фазе, то есть они достигают максимума и обращаются в нуль в одних и тех же точках. При этом если вектор
изменяются со временем по гармоническому закону, причем эти изменения происходят в одной фазе, то есть они достигают максимума и обращаются в нуль в одних и тех же точках. При этом если вектор 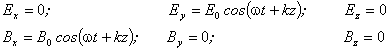 .
.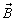 . Как показывает опыт, физическое, фотохимическое и другие действия света вызываются колебаниями электрического вектора. Поэтому в дальнейшем, говоря о световой волне, мы чаще будем говорить только о векторе напряженности электрического поля.
. Как показывает опыт, физическое, фотохимическое и другие действия света вызываются колебаниями электрического вектора. Поэтому в дальнейшем, говоря о световой волне, мы чаще будем говорить только о векторе напряженности электрического поля.


