Испускание электромагнитных волн происходит при ускоренном движении электрических зарядов. Простейшей моделью источника электромагнитных волн является электрический диполь, дипольный момент которого  гармонически изменяется со временем. Такой элементарный диполь называют диполем Герца. В радиотехнике диполь Герца эквивалентен небольшой антенне, размер которой много меньше длины волны. Примером такого диполя может служить система, образованная неподвижным точечным зарядом
гармонически изменяется со временем. Такой элементарный диполь называют диполем Герца. В радиотехнике диполь Герца эквивалентен небольшой антенне, размер которой много меньше длины волны. Примером такого диполя может служить система, образованная неподвижным точечным зарядом  и колеблющимся около него точечным зарядом
и колеблющимся около него точечным зарядом  . Такой «колеблющийся» диполь называют осциллятором, или элементарным вибратором. Осцилляторами широко пользуются в физике моделирования и расчета полей излучения реальных систем. Дипольный момент этой системы изменяется со временем по закону
. Такой «колеблющийся» диполь называют осциллятором, или элементарным вибратором. Осцилляторами широко пользуются в физике моделирования и расчета полей излучения реальных систем. Дипольный момент этой системы изменяется со временем по закону
 ,
,
где модуль вектора  – амплитуда колебаний заряда
– амплитуда колебаний заряда  .
.
Изучение такой излучающей системы имеет большое значение в связи с тем, что многие вопросы взаимодействия излучения с веществом могут быть объяснены классически, исходя из представления об атомах как о системах зарядов, в которых содержатся электроны, способные совершать гармонические колебания около положения равновесия. Кроме того, всякую реальную излучательную систему – антенну, по которой течет переменный ток, – можно мысленно разложить на элементы тока, каждый из которых излучает как диполь. Используя принцип суперпозиции для вектора напряженности электрического поля и вектора индукции магнитного поля, можно получить электромагнитное поле всей излучающей системы.
Рассмотрим излучение диполя, размеры которого малы по сравнению с длиной волны  . Будем считать, что диполь неподвижен. Начало координат поместим в точку нахождения диполя. Если бы дипольный момент был постоянным, то вектор напряженности электрического поля определялся бы формулой, полученной в электростатике:
. Будем считать, что диполь неподвижен. Начало координат поместим в точку нахождения диполя. Если бы дипольный момент был постоянным, то вектор напряженности электрического поля определялся бы формулой, полученной в электростатике:
 .
.
На малых расстояниях от диполя эта формула верна и в тех случаях, когда дипольный момент  меняется со временем. Но на больших расстояниях эта формула не может быть верной, так как на прохождение таких расстояний электромагнитному возмущению, распространяющемуся со скоростью
меняется со временем. Но на больших расстояниях эта формула не может быть верной, так как на прохождение таких расстояний электромагнитному возмущению, распространяющемуся со скоростью  , требуется конечное время
, требуется конечное время  , в течение которого дипольный момент
, в течение которого дипольный момент  может значительно измениться.
может значительно измениться.
Описание электромагнитного поля сильно упрощается в так называемой волновой зоне диполя, которая начинается на расстояниях, значительно превышающих длину волны  . Если волна распространяется в вакууме или в однородной изотропной среде, то волновой фронт в волновой зоне будет сферическим. Векторы
. Если волна распространяется в вакууме или в однородной изотропной среде, то волновой фронт в волновой зоне будет сферическим. Векторы 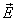 и
и 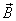 в каждой точке взаимно перпендикулярны и перпендикулярны к направлению распространения волны, то есть к радиус-вектору, проведенному в данную точку из центра диполя (рис. 1.6).
в каждой точке взаимно перпендикулярны и перпендикулярны к направлению распространения волны, то есть к радиус-вектору, проведенному в данную точку из центра диполя (рис. 1.6).
Назовем сечения волнового фронта плоскостями, проходящими через ось диполя, меридианами, а плоскостями, перпендикулярными к оси диполя, – параллелями. Тогда можно сказать, что 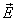 в каждой точке волновой зоны направлен по касательной к меридиану, а вектор
в каждой точке волновой зоны направлен по касательной к меридиану, а вектор 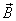 – по касательной к параллели. Если смотреть вдоль вектора
– по касательной к параллели. Если смотреть вдоль вектора  , то мгновенная картина будет как на рис. 1.6, при этом амплитуда при перемещении вдоль луча убывает.
, то мгновенная картина будет как на рис. 1.6, при этом амплитуда при перемещении вдоль луча убывает.
В каждой точке векторы 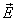 и
и 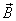 колеблются по закону
колеблются по закону  . Амплитуды
. Амплитуды  и
и  зависят от расстояния
зависят от расстояния  до излучателя и от угла
до излучателя и от угла  между направлением
между направлением  и осью диполя. Для вакуума
и осью диполя. Для вакуума  и
и  будут пропорциональны
будут пропорциональны  . Среднее значение плотности потока энергии примерно равно произведению
. Среднее значение плотности потока энергии примерно равно произведению  , следовательно,
, следовательно,  пропорционально
пропорционально  .
.
Из этой формулы вытекает, что при заданном значении угла  интенсивность волны изменяется вдоль луча обратно пропорционально квадрату расстояния от излучателя. Кроме того, она зависит от угла
интенсивность волны изменяется вдоль луча обратно пропорционально квадрату расстояния от излучателя. Кроме того, она зависит от угла  . Сильнее всего излучает диполь в направлениях, перпендикулярных к его оси, то есть при
. Сильнее всего излучает диполь в направлениях, перпендикулярных к его оси, то есть при  . Зависимость интенсивности от угла
. Зависимость интенсивности от угла  очень наглядно изображается с помощью диаграммы направленности диполя. Эта диаграмма строится так, чтобы длина отрезка, отсекаемого ею на луче, проведенном из центра диполя, давала интенсивность излучения под углом
очень наглядно изображается с помощью диаграммы направленности диполя. Эта диаграмма строится так, чтобы длина отрезка, отсекаемого ею на луче, проведенном из центра диполя, давала интенсивность излучения под углом  (рис. 1.7).
(рис. 1.7).

 гармонически изменяется со временем. Такой элементарный диполь называют диполем Герца. В радиотехнике диполь Герца эквивалентен небольшой антенне, размер которой много меньше длины волны. Примером такого диполя может служить система, образованная неподвижным точечным зарядом
гармонически изменяется со временем. Такой элементарный диполь называют диполем Герца. В радиотехнике диполь Герца эквивалентен небольшой антенне, размер которой много меньше длины волны. Примером такого диполя может служить система, образованная неподвижным точечным зарядом  и колеблющимся около него точечным зарядом
и колеблющимся около него точечным зарядом  . Такой «колеблющийся» диполь называют осциллятором, или элементарным вибратором. Осцилляторами широко пользуются в физике моделирования и расчета полей излучения реальных систем. Дипольный момент этой системы изменяется со временем по закону
. Такой «колеблющийся» диполь называют осциллятором, или элементарным вибратором. Осцилляторами широко пользуются в физике моделирования и расчета полей излучения реальных систем. Дипольный момент этой системы изменяется со временем по закону ,
, – амплитуда колебаний заряда
– амплитуда колебаний заряда  . Будем считать, что диполь неподвижен. Начало координат поместим в точку нахождения диполя. Если бы дипольный момент был постоянным, то вектор напряженности электрического поля определялся бы формулой, полученной в электростатике:
. Будем считать, что диполь неподвижен. Начало координат поместим в точку нахождения диполя. Если бы дипольный момент был постоянным, то вектор напряженности электрического поля определялся бы формулой, полученной в электростатике: .
. меняется со временем. Но на больших расстояниях эта формула не может быть верной, так как на прохождение таких расстояний электромагнитному возмущению, распространяющемуся со скоростью
меняется со временем. Но на больших расстояниях эта формула не может быть верной, так как на прохождение таких расстояний электромагнитному возмущению, распространяющемуся со скоростью  , требуется конечное время
, требуется конечное время  , в течение которого дипольный момент
, в течение которого дипольный момент 
 . Если волна распространяется в вакууме или в однородной изотропной среде, то волновой фронт в волновой зоне будет сферическим. Векторы
. Если волна распространяется в вакууме или в однородной изотропной среде, то волновой фронт в волновой зоне будет сферическим. Векторы 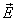 и
и 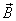 в каждой точке взаимно перпендикулярны и перпендикулярны к направлению распространения волны, то есть к радиус-вектору, проведенному в данную точку из центра диполя (рис. 1.6).
в каждой точке взаимно перпендикулярны и перпендикулярны к направлению распространения волны, то есть к радиус-вектору, проведенному в данную точку из центра диполя (рис. 1.6). , то мгновенная картина будет как на рис. 1.6, при этом амплитуда при перемещении вдоль луча убывает.
, то мгновенная картина будет как на рис. 1.6, при этом амплитуда при перемещении вдоль луча убывает. . Амплитуды
. Амплитуды  и
и  зависят от расстояния
зависят от расстояния  до излучателя и от угла
до излучателя и от угла  между направлением
между направлением  и
и  будут пропорциональны
будут пропорциональны  . Среднее значение плотности потока энергии примерно равно произведению
. Среднее значение плотности потока энергии примерно равно произведению  , следовательно,
, следовательно,  пропорционально
пропорционально  .
.
 . Зависимость интенсивности от угла
. Зависимость интенсивности от угла 


