Электромагнитные колебания.
1. ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Общие положения. Свободными затухающими колебаниями называются колебания, амплитуда которых из-за потерь энергии колебательной системой с течением времени уменьшается. Закон, по которому происходят колебания, зависит от свойств колебательной системы. Система называется линейной, если параметры, характеризующие существенные в рассматриваемом процессе физические свойства системы, не изменяются в ходе процесса. Линейными системами являются, к примеру, пружинный маятник при малых деформациях пружины, колебательный контур индуктивность, ёмкость и сопротивление которого не зависит ни от тока в контуре, ни от напряжения. Дифференциальное уравнение свободных затухающих колебаний линейной системы имеет вид:
где s - колеблющаяся величина, β = const - коэффициент затухания, ω0 - циклическая частота свободных незатухающих колебаний той же колебательной системы при отсутствии потерь энергии (при β = 0) называется собственной частотой колебательной системы. При не слишком сильном затухании (при β; < ω;0) общее решение уравнения (1.1) имеет вид:
где A 0 и φ; - произвольные постоянные, ω- величина, определяемая формулой:
На рисунке 1 дан график функции (1.2). Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки s.
В соответствии с видом функции (1.2) движение системы можно рассматривать как гармоническое колебание частоты
Верхняя из пунктирных кривых дает график функции A (t), причем величина А 0представляет собой амплитуду в начальный момент времени. Период затухания колебаний равен:
При незначительном сопротивлении среды (β; < ω;0) период колебаний практически не изменяется и равен
Последующие наибольшие отклонения в какую–либо сторону (например, Вообще, отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно:
Это соотношение называется декрементом затухания, а его натуральный логарифм – логарифмическим декрементом затухания.
Для характеристики колебательной системы обычно используется логарифмический декремент затухания. Выразив β; через δ; и Т, можно закон убывания амплитуды со временем записать в виде:
Таким образом, величина δ; определяет степень убывания амплитуды в течение одного периода. Важной характеристикой колебательной системы является добротность Q - безразмерная величина, равная произведению 2π на отношение энергии W (t) колебаний системы в произвольный момент времени t к убыли этой энергии за промежуток времени от t до (t + Т), то есть за один период колебания:
Так как энергия W(t) пропорциональна квадрату амплитуды колебаний A (t), то
При малых значениях логарифмического декремента затухания (δ; <<1) [1 – еxp(-2 δ;) ≈ 2 δ;] и добротность колебательной системы
(T принято равным Т 0, так как затухание невелико (β; << ω;0)).
Электромагнитные колебания. Колебательный контур состоит из конденсатора емкостью С катушки индуктивностью L и резистора сопротивлением R, соединенных между собой последовательно (рис. 2).
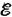 . Здесь U c - разность потенциалов на обкладках конденсатора в произвольный момент времени; . Здесь U c - разность потенциалов на обкладках конденсатора в произвольный момент времени; 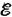 - ЭДС самоиндукции (в рассматриваемом контуре это единственная ЭДС); ток в контуре I и заряд на конденсаторе q связаны соотношением I = - (dq / dt). где q = CU c. знак «-» указывает на то, что положительным считается направление тока, соответствующее убыли заряда (разности потенциалов) на конденсаторе. - ЭДС самоиндукции (в рассматриваемом контуре это единственная ЭДС); ток в контуре I и заряд на конденсаторе q связаны соотношением I = - (dq / dt). где q = CU c. знак «-» указывает на то, что положительным считается направление тока, соответствующее убыли заряда (разности потенциалов) на конденсаторе.
Подставив значения
Решение уравнения (1.5) имеет вид
где ω - циклическая частота возникающего в контуре колебательного процесса; φ;0 - начальная фаза; β; = R/2L - коэффициент затухания колебаний. Разность потенциалов обкладок конденсатора изменяется по тому же закону, что и заряд:
График зависимости U c(t)(для φ;0 = 0) изображен на рис.3. Множитель A (t) = U 0 e-βt,
Рис.3
называемый амплитудой колебательного процесса, убывает по экспоненциальному закону (пунктирная линия на рис. 3); U 0 - начальная амплитуда. Величина ω; согласно (1.1), (1.3) и (1.5) определяется формулой
Из этого выражения следует, что свободные затухающие колебания возможны в контуре, сопротивление которого удовлетворяет условию
При этом переход электрической энергии в магнитную и обратно будет происходить с потерей на джоулево тепло. Если В отсутствие сопротивления (R = 0) в контуре возникают свободные незатухающие колебания с частотой
При этом энергия электрического поля конденсатора С полностью переходит в энергию магнитного поля катушки L и наоборот. При малых затуханиях (δ; <<1) для добротности контура из (1.4) следует:
2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДА
|

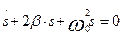 (1.1)
(1.1) (1.2)
(1.2) . (1.3)
. (1.3)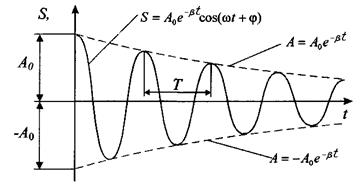
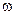 с амплитудой, изменяющейся по закону:
с амплитудой, изменяющейся по закону: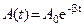 .
.
 .
. и т.д. на рис.) образуют геометрическую прогрессию. Действительно, если
и т.д. на рис.) образуют геометрическую прогрессию. Действительно, если  , то
, то  ,
, 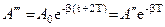 и т.д.
и т.д.

 .
.

 (1.4)
(1.4)
 (1.5)
(1.5)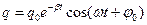
 , где
, где  .
.
 .
. или
или 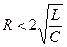
 , которую называют собственной частотой контура. Период таких колебаний
, которую называют собственной частотой контура. Период таких колебаний .
.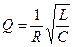 . (1.6)
. (1.6)


