Метод зон Френеля. Зонная пластинка
Согласно принципу Гюйгенса-Френеля световое поле в некоторой точке пространства является результатом интерференции вторичных источников. Френель предложил оригинальный и чрезвычайно наглядный метод группировки вторичных источников. Этот метод позволяет приближенным способом рассчитывать дифракционные картины, и носит название метода зон Френеля. Зоны Френеля вводятся следующим образом. Рассмотрим распространение световой волны из точки L в точку наблюдения P. Сферический волновой фронт, исходящий из точки L разобьем концентрическими сферами с центром в точке P и с радиусами z1 + λ/2; z1 + 2 λ/2; z1 + 3 λ/2… Полученные кольцевые зоны и носят название зон Френеля. Смысл разбиения поверхности на зоны Френеля состоит в том, что разность фаз элементарных вторичных волн, приходящих в точку наблюдения от данной зоны, не превышает π. Сложение таких волн приводит к их взаимному усилению. Поэтому каждую зону Френеля можно рассматривать как источник вторичных волн, имеющих определенную фазу. Две соседние зоны Френеля действуют как источники, колеблющиеся в противофазе, т.е вторичные волны, распространяющиеся из соседних зон в точке наблюдения будут гасить друг друга. Чтобы найти освещенность в точке наблюдения P нужно просуммировать напряженности электрических полей от всех вторичных источников, приходящих в данную точку. Результат сложения волн зависит от амплитуды и разности фаз. Так как разность фаз между соседними зонами равна P, то можно перейти к суммированию амплитуд. Амплитуда вторичной сферической волны пропорциональна площади элементарного участка, испускающего эту волну (т.е пропорциональна площади зоны Френеля). Кроме того, она убывает с увеличением расстояния z1 от источника вторичной волны до точки наблюдения по закону 1 / z1 и с ростом угла φ между нормалью к элементарному участку, испускающего волну, и направлением распространения волны. 19.Дифракция Френеля на круглом отверстии и диске. На круглом отверстии:
Сферическая волна, распространяющаяся из точечного источника монохроматического света S, встречает на своем пути экран с круглым отверстием, диаметр которого d=BC. Пусть Ф - фронт волны, который является частью поверхности сферы. Разобьем поверхность фронта на зоны Френеля так, что волны от соседних зон приходят в точку наблюдения М в противофазе. Тогда амплитуда результирующей волны в точке М. А=А1-А2+А3-А4+-Аm, где Аi - амплитуда волны, пришедшей от i-ой зоны Френеля. Перед Аm берется знак плюс, если m - нечетное, и минус, если m (число зон Френеля)- четное. На диске: пусть диск перекрывает 1-ое m зон, тогда амплитуда результирующей волны: А=Аm+1-Аm+2+Аm+3+…=Аm+1/2 и тогда, на экране всегда в центре будет наблюдаться максимум светлое пятно, вверх и вниз будут располагаться менее интенсивные максимумы более высоких порядков.
20.Дифракция Фраунгофера на бесконечно длинной щели. Дифракция Фраунгофера, имеющая большое практическое значение, наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызвавшего дифракцию. Чтобы этот тип дифракции осуществить, достаточно точечный источник света поместить в фокусе собирающей линзы, а дифракционную картину исследовать в фокальной плоскости второй собирающей линзы, установленной за препятствием. Рассмотрим дифракцию Фраунгофера от бесконечно длинной. Пусть плоская монохроматическая световая волна падает нормально плоскости узкой щели шириной а. Оптическая разность хода между крайними лучами, идущими от щели в произвольном направлении
где F — основание перпендикуляра, опущенного из точки на луч. разобьем эту пов-ть на зоны Френеля,тогда на отрезок FN будет укладыв. число зон Френеля
Если открывается нечетное число зон Френ. в данной точке будет наблюд. максимум. Условие максимума: Если
21 Одномерная дифракционная решетка представляет собой систему большого числа N одинаковых по ширине b и параллельных друг другу щелей, разделенных одинаковыми по ширине а промежутками. Величина d=a+b называется постоянной (периодом) дифракционной решетки.
|



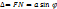
 .Если открыто четное число зон Френ.,то волны от этих зон компенсируют друг друга и в выбранной точке будет наблюдаться минимум.
.Если открыто четное число зон Френ.,то волны от этих зон компенсируют друг друга и в выбранной точке будет наблюдаться минимум.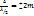 .
.  - это условие минимума на ДК.m – порядок минимума.
- это условие минимума на ДК.m – порядок минимума. .
. , то это сообветсявует одной открытой зоне Френ.В центре будут наблюд. главный максимум нулевого порядка.
, то это сообветсявует одной открытой зоне Френ.В центре будут наблюд. главный максимум нулевого порядка.


