Исходные данные. 1. Шамис В.А. Borland C++ Builder. Программирование на С++ без проблем
1. Шамис В.А. Borland C++ Builder. Программирование на С++ без проблем. М.:”Нолидж”, 1997 – 266 с. 2. Елманова Н.Э., Кошель С.П. Введение в Borland C++ Builder4 -М.: Диалог-МИФИ, 1999 - 352 с. 3. Архангельский А.Я. Программирование в Borland C++ Builder 4 - М.: ЗАО Издательство "БИНОМ", 1999 - 928 с. Порядок выполнения работы 1. Ознакомиться с методическими указаниями. 2. Получить у преподавателя постановку задачи. 3. Осуществить полную предмашинную подготовку задачи. 4. Выполнить машинную обработку полученных программ. 5. Проанализировать полученные результаты. 6. Оформить техническую документацию (отчёт). 7. Защитить работу. Предмашинная подготовка задачи Ветвящимся (разветвляющимся) называется процесс с выбором одного из возможных вариантов вычислений в зависимости от проверки заданных условий. Условие – зависимость, формирующая узел ветвления. Узелветвления – точка преобразования исходной (входной) ветви в несколько формируемых (выходных). Ветвь – каждый из возможных вариантов решения. Простой(простое ветвление) – разветвляющийся процесс, содержащий две выходные ветви. По сложности условия простые ветвления делятся на элементарные и составные (рис. 2). Элементарное (простейшее) – условие, требующее проверки одной операции отношения . Рассмотрим программирование элементарного ветвящегося вычислительного процесса на конкретной задаче об удельных нагрузках. Постановка задачи На складе сырья химкомбината имеются две ёмкости. Первая из них расположена на квадратном основании, вторая – на цилиндрическом. Рассчитать удельную нагрузку на основание при условии, что партия сырья объёмом 15 м3 должна заливаться в первую ёмкость, если масса полученного продукта меньше или равна 14,85 т, или во вторую, если масса продукта больше 14,85 т. Плотность сырья может изменяться в диапазоне от 0,963 т/м3 до 1,15 т/м3. Длина стороны квадрата равна 296 см, диаметр цилиндра – 2,65 м. Формирование математической модели Исходные данные
Расчётные зависимости
Дополним каждую расчётную зависимость её возможным номером (например n) с конкретным значением и представим всё в общепринятой форме:
|

 = _,_ _ _ т/м3
= _,_ _ _ т/м3
 = 3,1416
= 3,1416
 [
[  ] – масса поступившего сырья;
] – масса поступившего сырья; [
[  ], если
], если  – удельная нагрузка на квадратное основание;
– удельная нагрузка на квадратное основание; [
[  ], если
], если 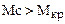 – удельная нагрузка на цилиндрическое основание.
– удельная нагрузка на цилиндрическое основание.



