Общие сведения. Рассмотрим тело, закрепленное на оси спиральной пружины
Рассмотрим тело, закрепленное на оси спиральной пружины. Если повернуть тело на некоторый угол j, то вследствие закручивания пружины возникнет упругая сила. Эта сила создает крутящий момент М, возвращающий систему в исходное состояние, и возникнут крутильные колебания. Крутящий момент М пропорционален углу поворота j
где D - модуль кручения, зависящий от механических свойств пружины. Если пренебречь силами сопротивления, то основное уравнение динамики вращательного движения имеет вид
где J – момент инерции, e - угловое ускорение.
Из уравнений (1) и (2) и с учетом (3) следует
Это уравнение можно переписать в виде
Введем обозначения
Тогда уравнение (5) примет вид
Это дифференциальное уравнение крутильных колебаний. Решением этого уравнения являются функции синуса ил косинуса (гармонические функции)
где jо – максимальное (амплитудное) значение угла поворота, wо – круговая (циклическая) частота, a - начальная фаза. Таким образом, крутильные колебания являются гармоническими колебаниями.
Если в системе имеются силы трения, то амплитуда колебаний будет постепенно уменьшаться, то есть колебания будут затухающими. За счет сил трения возникает тормозящий момент
где r – коэффициент сопротивления, Тогда основное уравнение динамики вращательного движения запишется так
Введя обозначения
получим дифференциальное уравнение затухающих колебаний
Решением этого уравнения является следующая функция
b - коэффициент затухания
Она уменьшается с течением времени.
Степень затухания характеризуется несколькими величинами – коэффициентом затухания Логарифм отношения двух последовательных значений амплитуд, отстоящих друг от друга на время, равное периоду T, называется логарифмическим декрементом затухания.
l=bT (11) Время
bt=1 (12)
|

 (1)
(1) (2)
(2) (3)
(3)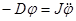 (4)
(4) (5)
(5)
 (6)
(6)

 Частота и период этих колебаний равны соответственно
Частота и период этих колебаний равны соответственно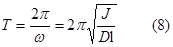
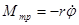
 - угловая скорость.
- угловая скорость.




 (9)
(9)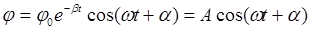
 - амплитуда затухающих колебаний.
- амплитуда затухающих колебаний. частота затухающих колебаний
частота затухающих колебаний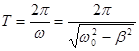 период затухающих колебаний
период затухающих колебаний Затухающие колебания представляют собой непериодические колебания, так как в них значения смещения, скорости, ускорения не повторяются через период. Так что о периоде Т можно говорить лишь условно, как о времени, через которое система проходит через положение равновесия.
Затухающие колебания представляют собой непериодические колебания, так как в них значения смещения, скорости, ускорения не повторяются через период. Так что о периоде Т можно говорить лишь условно, как о времени, через которое система проходит через положение равновесия. , логарифмическим декрементом затухания
, логарифмическим декрементом затухания  , временем релаксации
, временем релаксации  .
. (10)
(10)
 - коэффициент затухания есть физическая величина обратная времени релаксации.
- коэффициент затухания есть физическая величина обратная времени релаксации.


