Введение. Лучшие компании кадрового рынка:
Лучшие компании кадрового рынка: • ТРЕНИНГОВЫЕ компании • КАДРОВЫЕ агентства • КОНСАЛТИНГОВЫЕ компании • Организации, предлагающие ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ для HR-отделов • СТРАХОВЫЕ КОМПАНИИ. ФИТНЕС-КЛУБЫ . Организаторы КОРПОРАТИВНЫХ ПРАЗДНИКОВ • ЯЗЫКОВЫЕ ШКОЛЫ • ИЗДАТЕЛЬСТВА, публикующие специализированную литературу www.HRM.ru
ФИЗИКА Механические колебания МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНЫМ РАБОТАМ по дисциплине «Физика» Работы 4, 5, 5а, 105 МОСКВА - 2012
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛБНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»
Кафедра «Физика»
ФИЗИКА
Механические колебания
Под редакцией доцента В.А. Селезнева
Рекомендовано редакционно-издательским советом университета в качестве методических указаний для студентов ИУИТ, ИТТСУ, ИЭФ, ИПСС
МОСКВА - 2012
УДК 534 Л 97
Лагидзе Р.М., Лямзова И.А. Физика. Механические колебания. Методические указания к лабораторным работам по физике. Работы 4, 5, 5а, 105. / Под редакцией доцента В.А. Селезнева. – М.: МИИТ, 2012. – 32 с.
Методические указания к лабораторным работам по физике № 4, 5, 5а, 105 соответствуют программе и учебным планам по курсу общей физики (раздел «Колебания и волны») и предназначены для студентов всех специальностей.
ã МИИТ, 2012
Работа 4
ИЗУЧЕНИЕ СВОБОДНЫХ КОЛЕБАНИЙ ПРУЖИННОГО МАЯТНИКА
Цель работы: Определение коэффициента жесткости пружины по удлинению пружины и методом колебаний пружинного маятника.
Введение
Рассмотрим простейшую колебательную систему: груз массой m, подвешенный на пружине. Упругая сила растяжения пружины в положении равновесия равна силе тяжести груза и, будучи направлена вверх, уравновешивает ее. При выведении груза из положения равновесия пружина действует на него с дополнительной силой F, пропорциональной смещению x (при малых смещениях) и направленной в сторону противоположную смещению:
F = – kx,
где k – коэффициент жесткости пружины; он равен численному значению силы, которую нужно приложить к пружине, чтобы растянуть (или сжать) ее на единицу длины. Единица измерения коэффициента жесткости – [ k ] = Н×м-1. Груз, выведенный из положения равновесия, начнет совершать относительно него гармонические колебания:
x = A sin (ω t + φ0), (1)
где А – амплитуда колебания; (ω t + j0) – фаза колебания; ω – круговая частота; j0 – начальная фаза колебания. Энергия, сообщенная системе пружина-груз при начальном толчке, будет периодически преобразовываться: потенциальная энергия упруго деформированной пружины Е П = Согласно закону сохранения энергии для консервативной системы механическая энергия E = Е П + Е К= В момент прохождения грузом положения равновесия (x = 0) из формулы (2) следует, что полная энергия системы E = Е К max = Согласно уравнению (1), скорость гармонически колеблющегося груза u = а максимальная скорость u max = ω A. (3)
В крайних положениях груза (u = 0, x = ± A) энергия системы переходит полностью в потенциальную Е п:
E = Е П max = По закону сохранения энергии
Подставляя выражение (3) в соотношение (4), получим m ω2 = k, ω = Учитывая, что ω = T = 2p Таким образом, период не зависит от амплитуды колебаний и определяется только величинами m и k. Амплитуда и начальная фаза колебаний j0 определяются начальными условиями, при которых возникло движение. Приборы и принадлежности. Штатив с пружиной и зеркальной шкалой, держатель для грузов, набор грузов, секундомер.
Порядок выполнения работы
I. Определение коэффициента жесткости пружины k по удлинению пружины
1. Подвесить к концу пружины держатель (рис. 1).
Рис. 1
2. Пользуясь зеркальной шкалой, заметить начальное положение держателя l 0 (отсчет делают таким образом, чтобы нижняя грань держателя совпала с его зеркальным изображением) и записать данные отсчета в таблицу 1.
3. Постепенно нагружать держатель грузами (их масса в граммах маркирована на них), записывая положение нижней грани держателя l 1 для каждого значения растягивающей силы, соответствующей общей массе m грузов (масса держателя в m не входит).
4. Нагрузив держатель всеми грузами, начинают их по одному снимать, записывая в таблицу в обратном порядке снизу-вверх соответствующее положение нижней грани держателя l 2 для каждого значения m.
5. Вычислить среднее арифметическое величин l 1 и l 2 для каждой массы l СР =
6. Вычислить удлинение пружины для каждого значения массы грузов вычитая l 0 из соответствующего l СР: Δ l = l СР – l 0.
Таблица 1
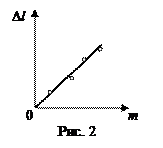
7. Построить проходящий через начало координат график зависимости удлинения пружины Δ l от массы m (рис. 2).
8. Рассчитать погрешность определения коэффициента жесткости по формуле D k = k Для расчета погрешности следует использовать те значения m и Δ l, по которым рассчитывался коэффициент жесткости, а в качестве Δ(Δ l), Δ m и Δ g взять приборную погрешность измерения удлинения и учесть точность, с которой задаются массы грузов и ускорение свободного падения. Результат расчета k и погрешности его определения Δ k занести в таблицу 1, выполнив предварительно соответствующее округление [4].
II. Определение коэффициента жёсткости k пружины по зависимости периода собственных колебаний пружинного маятника от массы груза
1. Поместить на держатель груз. Значение массы груза с держателем M и результаты последующих измерений занести в таблицу 2. Измерить секундомером время 10 полных колебаний маятника. Опыт повторить не менее 4 раз. Найти среднее значение времени t ср 10 полных колебаний и среднее значение периода колебаний Т СР =
2. Подобные измерения провести для различных значений грузов. Таблица 2
III. Определение коэффициента жесткости пружины методом колебаний
1. По результатам проведенных измерений построить проходящий через начало координат график зависимости квадрата периода колебаний Т 2 от массы M, предварительно рассчитав Т ср2 для каждого значения M. Выбрав одну из полученных в эксперименте точек, лежащую на усредненной прямой, рассчитать коэффициент жесткости пружины по формуле k СР = 4p2 2. Оценить погрешность полученного результата. При условии, что ошибка в определении числа колебаний отсутствовала, эту погрешность можно рассчитать по формуле D k = k В качестве Ошибка определения времени колебаний определяется как
D t =
Систематическую погрешность в определении времени Δ t СИСТ, связанную с конечной скоростью реакции человека, можно принять равной 0,1 с: t = t СЛ + t СИСТ. Случайную ошибку Δ t СЛ следует рассчитать по методу Стьюдента:
Δ t СЛ = a n , P
Для числа колебаний N = 4 и доверительной вероятности P = 0,95 коэффициент Стьюдента a n , P = 3,2. Окончательный результат записать в таблицу 2. Сравнить полученное значение коэффициента жесткости пружины с результатом, полученным ранее по методу измерения удлинения пружины (часть I).
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Какие деформации называются упругими? Сформулируйте закон Гука. 2. Какие колебания называются свободными? 3. Получите формулу для периода колебаний пружинного маятника. 4. Чем можно объяснить различие в значениях коэффициента жесткости, полученных разными методами?
Список литературы
1. Детлаф А.А., Яворский Б.М. Курс физики. –М.: Высш. шк. – 2000. 2. Савельев И.В. Курс физики. – Т. 2. – М.: Наука – 1998 и далее. 3. Трофимова Т.И. Курс физики. – М., 2000 и далее. 4. Селезнёв В.А., Тимофеев Ю. П. Вводное занятие в лабораториях кафедры физики. – М.: МИИТ. – 2011. – 38 с.
Работа 5 ИЗУЧЕНИЕ СВОБОДНЫХ КОЛЕБАНИЙ ФИЗИЧЕСКОГО МАЯТНИКА
Цель работы. Определение момента инерции физического маятника по периоду его малых колебаний и приведенной длине.
|


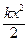 будет переходить в кинетическую энергию движущегося груза Е К =
будет переходить в кинетическую энергию движущегося груза Е К = 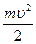 и обратно.
и обратно. +
+  = const. (2)
= const. (2)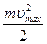 .
. = A ω cos (ω t + j0),
= A ω cos (ω t + j0),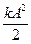 .
. .
. , получим выражение для периода колебаний Т:
, получим выражение для периода колебаний Т: . (5)
. (5)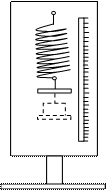
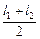 .
.
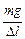 , взяв значения m и Δ l для любой точки усредненной прямой.
, взяв значения m и Δ l для любой точки усредненной прямой.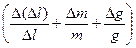 .
.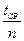 , где n = 10, при расчетах оставляя на одну значащую цифру больше, чем в результатах наблюдений.
, где n = 10, при расчетах оставляя на одну значащую цифру больше, чем в результатах наблюдений.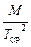 .
.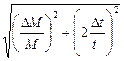 .
.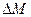 принимается точность, с которой задаются масса держателя и грузов.
принимается точность, с которой задаются масса держателя и грузов. .
.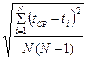 .
.


