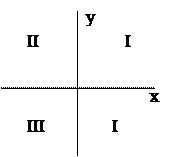Разветвляющиеся программы

2. Разработать программу вычисления интервальной функции с использование оператора IF…THEN, заданной графически на рис. 6.

3. Треугольник задан сторонами А, В и С. Разработать программу, определяющую, является ли он равносторонним, равнобедренным или разносторонним.

4. Треугольник задан своими сторонами А, В и С. Определить, является ли он прямоугольным (использовать условие равенства квадрата гипотенузы сумме квадратов катетов).

5. Определить, попадает ли точка с координатами Х ₀, Y ₀под кривую функции y = cos x, заданную в интервале 0 ≤ Х ≤ 2π.

6. Даны четыре числа A, B, C, D. Разработать программу определения максимального числа.

 

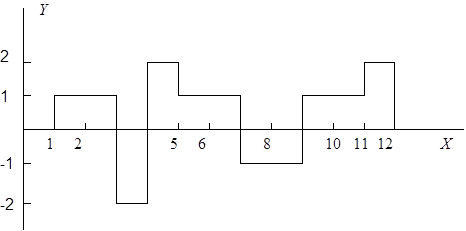
Рис. 6

 

7. Квадратное уравнение задано коэффициентами a, b и c. Разработать программу для вычисления корней этого уравнения. В случае, если корней нет, выдать сообщение об этом на экран.

8. Дана точка M с координатами Х _O, Y _O. Разработать программу для определения номера квадранта (четверти), в котором будет находиться точка.

 

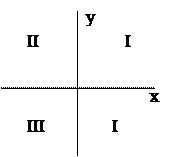
Рис. 7

 

9. Дана точка с координатами Х ₀, Y ₀. Разработать программу, определяющую, попадает ли точка с координатами Х ₀, Y ₀ в квадрат, изображенный на рис. 8.

10. Определить, попадает ли точка с координатами Х ₀, Y ₀ в круг с радиусом, равным 2 (уравнение окружности r ² = х ² + y ²).

 

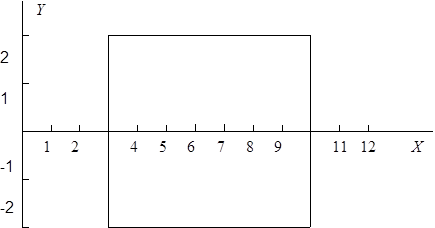
Рис. 8

 

11. Составить программу нахождения значения Q при заданных произвольных значениях x, y, z.

 

Х >0	Х ≤0
Y >0	Y ≤0	Y >0	Y ≤0
Z >0	Z ≤0	Z >0	Z ≤0	Z>0	Z ≤0	Z >0	Z ≤0
Q =1	Q =2	Q =3	Q =4	Q= 5	Q =6	Q =7	-Q =8

 

12. Даны три различных целых числа. Определить, какое из них (первое, второе или третье):

а) самое большое;

б) самое маленькое;

в)является средним (средним назовем число, которое боль­ше наименьшего из данных чисел, но меньше наибольшего).

13. Определить максимальное и минимальное значения из трех различных вещественных чисел.

14. Составить программу нахождения суммы двух наиболь­ших из трех различных чисел.

15. Составить программу нахождения произведения двух наименьших из трех различных чисел.

16. Даны две тройки вещественных чисел. В каждой трой­ке все числа различные. Найти среднее арифметическое сред­них чисел каждой тройки (средним назовем такое число в тройке, которое больше наименьшего из чисел данной трой­ки, но меньше наибольшего).

17. Составить программу, которая в зависимости от по­рядкового номера дня недели (1, 2,..., 7) выводит на экран его название (понедельник, вторник,..., воскресенье).

18. Составить программу, которая в зависимости от по­рядкового номера месяца (1, 2,..., 12) выводит на экран его название (январь, февраль,..., декабрь).

 

Контрольные вопросы

 

1. Поясните, как работает структура разветвления.

2. Какие две формы записи имеет оператор If … Then?

3. Чем отличается блочный синтаксис оператора If … Then от линейного синтаксиса?

4. Поясните алгоритм работы блочной формы оператора If … Then.

5. Поясните алгоритм работы линейной формы оператора If … Then.

6. Как связываются между собой несколько условий в операторе If … Then.?

7. Перечислите логические функции и кратко охарактеризуйте каждую из них.

8. Для чего используется оператор Select Case?

9. Поясните работу оператора Select Case.

10. Как могут быть записаны сложные выражения в списке выражений оператора Select Case?

11. Как организовать ветвление с использование функции MsgBox?

12. В чем преимущество организации ветвления с помощью функции MsgBox?

 

 

_____________________________

 

 

Рекомендуемая литература

 

1. Кузьменко В. Г. VBA 2002. М.: ЗАО "БИНОМ", 2002.

2. Мамонтов Д. В. Quick Basic в задачах и примерах. СПб.: Питер, 2006.

3. Гусева А. И. Учимся информатике: задачи и методы их решения. М.: "Диалог-МИФИ", 1998.

4. Зельднер Г. А. Программируем на языке QuickBASIC 4.5. М.: ABF, 1996.

5. Зельднер Г. А. Microsoft BASIC Professional Development System 7.1. Руководство программиста. М.: ABF, 1996.

6. Алиев В. К. Языки Basic. М.: Солон-Р, 2000

7. Назаров С. В., Мельников П. П. Программирование на MS Visual Basic. М.: Финансы и статистика, 2002.

 

 

Валерий Валентинович Косулин

Ольга Вячеславовна Рябова

 

 

ОСНОВЫ РАБОТЫ В VBA. АЛГОРИТМЫ С РАЗВЕТВЛЯЮЩЕЙСЯ СТРУКТУРОЙ

Лабораторная работа по курсу

"Информатика"

(Кафедра Информатики и информационных управляющих систем КГЭУ)

 

Редактор издательского отдела Н. И. Андронова

________________________________________________________________

Изд. лиц. № 03480 от 8.12.00 Темплан издания КГЭУ 2007 г.

Подписано к печати Формат 60 х 84/16

Гарнитура “Times” Вид печати РОМ Бумага “Business”

Физ. печ. л. Усл. печ. л. Уч-изд. л.

Тираж 100 Заказ

________________________________________________________________

Издательский отдел КГЭУ

420066, Казань, Красносельская, 51

________________________________________________________________

Типография КГЭУ

420066, Казань, Красносельская, 51

 

Разветвляющиеся программы

1)	Даны действительные числа x, y. Определить, принадлежит ли точка с координатами геометрической фигуре: ромб с вершинами в точках (0,1), (1,0), (0,-1), (-1,0).
2)	Даны действительные числа x, y. Определить, принадлежит ли точка с координатами геометрической фигуре: черырехугольник с вершинами (0,1), (0.5,0), (0,-1),(-0.5,0).
3)	Даны действительные числа x, y. Определить, принадлежит ли точка с координатами геометрической фигуре: фигура, состоящая из треугольника с вершинами в точках (-2,0), (0,1), (0,-1) и правого полукруга радиуса R с центром в начале координат.
4)	Даны действительные числа x, y. Определить, принадлежит ли точка с координатами геометрической фигуре: треугольник с вершинами (-1,-1), (1,-1), (0,2).
5)	Даны действительные числа x, y. Определить, принадлежит ли точка с координатами геометрической фигуре: пятиугольник с вершинами (0,0), (1,1), (1,-2), (-1,-2), (-1,1).
6)	Даны действительные числа x, y. Определить, принадлежит ли точка с координатами геометрической фигуре: четырехугольник с вершинами (0,0), (1,0), (-2,-1), (1,-2).
7)	Даны действительные числа x, y. Определить, принадлежит ли точка с координатами геометрической фигуре: верхняя часть плоскости, ограниченной ломаной линией, проходящей через точки (-∞,1),(-1,1),(0,0),(1,1),(∞,1).
8)	Определить, лежит ли заданная точка на одной из сторон треугольника, заданного своими вершинами.
9)	Станции A, B, C расположены на n-том, m-том и p-том километрах железной дороги, соответственно. Какие из этих станций расположены наиболее близко друг к другу.
10)	Даны действительные числа x и y. Меньшее из этих двух чисел заменить их полусуммой, а большее – их удвоенным проведением.
11)	Даны действительные числа x, y. Определить, принадлежит ли точка с координатами геометрической фигуре: область, ограниченная кривыми, заданными выражениями y=abs(x) и x2+y2=1.
12)	Определить, пройдет ли кирпич с ребрами a, b, c в прямоугольное отверстие со сторонами x и y.
13)	Даны действительные числа x, y. Определить, принадлежит ли точка с координатами геометрической фигуре: нижняя часть полуокружности, заданной уравнением x2+y2=1 и прямой y=x/2.
14)	Заданы площади круга и квадрата. Определить, поместиться ли квадрат в круге.
15)	Даны действительные числа x, y. Определить, принадлежит ли точка с координатами геометрической фигуре: круг радиуса 1 с центром в точке (0,1) (x2+(y-1)2<1) и треугольник с координатами вершин (0,1), (-1,0), (1,0).
16)	Выяснить можно уместить прямоугольник со сторонами a,b уместить внутрь прямоугольника c,d.
17)	Даны действительные числа x, y. Определить, принадлежит ли точка с координатами геометрической фигуре: область, ограниченная кривыми, заданными выражениями x2+(y-1)2=1 и y=1-x2.
18)	Даны действительные числа x, y. Определить, принадлежит ли точка с координатами геометрической фигуре: область, ограниченная кривыми, заданными выражениями y=ex, y=e-x, y=x2.
19)	Даны действительные числа a, b, c (a<>0). Выяснить, имеет ли уравнение ax2+bx+c=0 действительные корни. Если корни имеются, то найти их. В противном случае ответом должно служить сообщение, что действительных корней нет.
20)	Даны действительные числа x, y. Определить, принадлежит ли точка с координатами геометрической фигуре: два круга радиуса 1 с центрами в точках (-1,0) и (1,0).
21)	Даны действительные числа x, y. Определить, принадлежит ли точка с координатами геометрической фигуре: треугольник с координатами вершин (-1,1), (1,1) и (0,0) и круг с центром в точке (0,-1) и радиусом 1.
22)	Даны действительные числа x, y. Определить, принадлежит ли точка с координатами геометрической фигуре: два треугольника с вершинами в точках (-1,1), (-1,-1), (0,0) и (1,1), (-1,1), (0,0).
23)	На карте координаты начала и конца строящегося прямолинейного участка дороги обозначены как (x1,y1) и (x2,y2). Карьер, откуда можно брать гравий для стройки имеет координаты (x0,y0). Определить минимальное расстояние от строящегося участка шоссе до карьера.
24)	Определить номер квадранта, в котором нходится точка, задання координатами (x,y).
25)	Определить, имеются ли среди цифр заданного целого трехзначного числа одинаковые
26)	Определить, лежат ли две точки заданные своими координатами окружности с центром в начале координат.
27)	Определить, есть ли в заданном целом трехзначном числе цифры, кратные друг другу.
28)	Числа a, b – катеты одного треугольника, c,d – катеты другого треугольника. Определить подобны ли эти треугольники.
29)	На карте координаты начала и конца строящегося прямолинейного участка дороги обозначены как (x1,y1) и (x2,y2). Карьер, откуда можно брать гравий для стройки имеет координаты (x0,y0). Определить максимальное расстояние от строящегося участка шоссе до карьера.
30)	Заданы площади круга и квадрата. Определить, поместиться ли круг в квадрате.