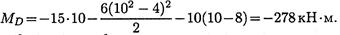Решение. Задачу решаем с помощью составления уравнений поперечных сил и изгибающих моментов в поперечных сечениях балки.
Задачу решаем с помощью составления уравнений поперечных сил и изгибающих моментов в поперечных сечениях балки. При проверке эпюр используем дифференциальные зависимости между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом: 1. Производная от поперечной силы по длине балки равна интенсивности распределенной нагрузки
2. Производная изгибающего момента по длине балки равна поперечной силе
Рассмотрим участок 1, сечение 1. Поперечная сила Q1 = - F1 = —15 кН. По принятому правилу знаков поперечная сила отрицательна и постоянна на этом участке. Изгибающий момент MXl = — F1 z1. 0 ≤ z1 ≤ 4м: МА = 0; МВ = -15*4 = - 60кН*м.
Рассмотрим участок 2, сечение 2. Поперечная сила Q2 = — F1 — q(z2 — 4). 4м ≤ z2 ≤ 8м: QB = - F1 = -15кН;
Поперечная сила изменяется по линейному закону.
Изгибающий момент : 4м ≤ z2 ≤ 8м: при z2 = 4м изгибающий момент МВ = — 60кН • м. В точке В нет внешнего момента, поэтому изгибающий момент слева и справа от точки В одинаков. В этом случае рассчитывать его дважды не следует;
Рассмотрим участок 3, сечение 3. В точке С приложена внешняя сила F 2. На эпюре должен быть скачок, равный приложенной силе; на эпюре моментов должен быть излом. Поперечная сила на участке 3: Q3 = —F1 — q(z3 — 4) — F2;
при z3 = 10 м QD = -15 – 6*6 - 10 = - 61 кH. Поперечная сила изменяется по линейному закону. Изгибающий момент.
8 м ≤ z2 ≤ 10 м: при z3 = 10 м
На участках 2 и 3 эпюра изгибающих моментов ограничена квадратичной параболой. По полученным результатам, учитывая дифференциальные зависимости между поперечной силой и изгибающим моментом, строим эпюры Q и Мх. На втором и третьем участках поперечная сила не имеет нулевых значений, поэтому на эпюре моментов нет экстремумов.
|