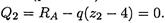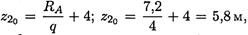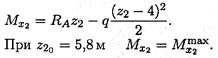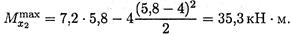Рассмотрим участок 1 до сечения 1.

В опоре А действует сосредоточенная сила R_A = 7,2 кН. На участке 1 поперечная сила остается постоянной: Q₁ = Ra = 7,2 кН (рис. 31.3).

Изгибающий момент в точке А равен нулю, т. к. здесь нет мо­мента внешней пары сил: М_А = 0.

Момент в точке С (граница участка, z = 4м) М_С = Ra * 4; Мс = 7,2 • 4 = 28,8кН • м.

Эпюра очерчивается прямой линией, наклонной к оси Oz (рис. 31.3).

Рассмотрим участок 2 (рис. 31.3). Здесь действует распределен­ная нагрузка интенсивностью q = 4кН/м. При перемещении вдоль оси балки направо распределенная нагрузка суммируется. Эпюра Q₂ — прямая линия, наклонная к оси Oz. Распределенная нагруз­ка направлена вниз (см. Основные правила построения эпюр, п. 4), здесь эпюра изгибающего момента очерчена параболой, обращенной выпуклостью вверх.

Реакция в опоре Ra и распределенная нагрузка направлены в разные стороны. Следовательно, возможна точка, в которой, по пра­вилу 2, Q₂ = 0, а изгибающий момент экстремален.

Для построения эпюры моментов необходимо составить уравне­ние поперечной силы на участке 2 и приравнять величину попереч­ной силы нулю. Из уравнения можно определить координату точки, в которой изгибающий момент экстремален.

Проводим необходимые расчеты, определяем величины попереч­ных сил и изгибающих моментов в характерных точках.

Рассмотрим участок 2, сечение 2 (рис. 31.3).

Уравнение поперечной силы

Откуда:

z₂₀ — координата точки, где изгибающий момент экстремален, т. к. Q₂ = 0.

Уравнение момента на участке 2:

Максимальное значение изгибающего момента на участке 2

Значения поперечной силы и изгибающего момента в точке В: Q_B = RB = 16,8кН; М_В = 0.

Строим эпюру поперечной силы. Первый участок — прямая ли­ния, параллельная оси Oz. В точке С эпюра становится наклонной. Строим эпюру изгибающих моментов (рис. 31.3).

Участок 1 эпюра — прямая линия; Ма = 0; Мс = 28,8 кН*м.

Участок 2 эпюра — парабола с экстремумом в точке z = 5,8 м; М _z ^mах = 35,3кН*м; М_В = 0.

 

Пример 3. Построить эпюры Q_y и М_х для бал­ки, изображенной на рис. 2.51, а.