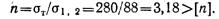Решение. Вырезая узел, в котором сходятся стержни, и составляя уравнения равновесия для действующих на него сил (рис

Вырезая узел, в котором сходятся стержни, и составляя уравнения равновесия для действующих на него сил (рис. 2.86)

устанавливаем, что заданная система статически неопре­делима (три неизвестных усилия и два уравнения ста­тики). Ясно, что для расчета стержней на прочность и устойчивость необходимо знать величины продольных сил, возникающих в их поперечных сечениях, т. е. нужно раскрыть статическую неопределимость.

 

Составляем уравнение перемещений на основе диа­граммы перемещений (рис. 2.87):

или, подставляя значения изменений длин стержней, по­лучаем

откуда

Решив это уравнение совместно с уравнениями ста­тики, найдем:

 

Напряжения в поперечных сечениях стержней 1 и 2 (см. рис. 2.86):

Их коэффициент запаса прочности

 

Для определения коэффициента запаса устойчивости стержня 3 надо вычислить критическую силу, а это тре­бует определения гибкости стержня, чтобы решить, какой формулой для нахождения N_Kp следует воспользоваться.

Итак, λ₀ < λ < λ_пред и крити­ческую силу следует определять по эмпирической формуле:

Коэффициент запаса устой­чивости

Таким образом, расчет пока­зывает, что коэффициент запаса устойчивости близок к требуемо­му, а коэффициент запаса проч­ности значительно выше требуемого, т. е. при увеличении нагрузки системы потеря устойчивости стержнем 3 вероят­нее, чем возникновение текучести в стержнях 1 и 2.