Линейные колебания в системах с одной степенью свободы.
Будем изучать основные закономерности таким колебаний. Примеры: математический маятник, физический маятник – в обоих случаях единственная переменная описывающая положение системы в данный момент времени – угол Динамические уравнения колебательного движения.
Физический маятник и торсионный пружинный осциллятор. Физический маятник:
Канонический вид уравнения:
Математический маятник – точечная масса на невесомом подвесе. Точка тела, лежащая на линии соединения точки подвеса и центра масс и удаленная от точки подвеса на расстояние Теорема Гюйгенса: если точку подвеса и центр качаний поменять местами («оборотный маятник»), частота колебаний маятника не изменится. Доказательство: Покажем, что приведенная длина прямого и оборотного маятника одинаковы:
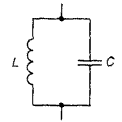
В условиях малых колебаний Колебательный контур:
Системы, описываемые одним и тем же дифференциальным уравнением, являются динамически эквивалентными. Качественно, они проявляют одни и те же закономерности поведения. Изучим их на какой-то одной системе. Пружинный маятник. Происходит превращение кинетической энергии груза в потенциальную энергию деформированной пружины и обратно. Физический маятник – превращение кинетической энергии маятника в потенциальную гравитационную энергии и обратно. Решение канонического уравнения (проверяется непосредственной подстановкой):
Важно: амплитуда и начальная фаза колебаний определяются начальными условиями: положением и скорость осциллятора в начальный момент времени
не зависит от амплитуды колебаний и начальных условий. Это свойство независимости периода колебаний от их амплитуды формулируют как изохронность колебаний: колебания с разными амплитудами имеют один и тот же период. Изохронность – атрибут линейного осциллятора. В этом смысле линейный осциллятор - сам себе часы. Он создает естественную для него единицу времени период собственных колебаний. Современный эталон времени – тоже колебательный процесс, а единица времени – связана с периодом этих эталонных колебаний. Примеры начальных условий:
Уравнение колебаний при данных начальных условиях: Другой способ задания начальных условий:
Уравнение колебаний при данных начальных условиях: При Общий случай произвольных начальных условий изучить самостоятельно. Энергетические превращения.
Потенциальная энергия силы упругости сжатой (растянутой) пружины равна половине квадрата ее деформации на коэффициент жесткости.
Последнее равенство отражает закон сохранения механической энергии в системе, когда в ней отсутствуют диссипативные силы. Заметим: Энергия колеблется с частотой, вдвое большей, чем меняется смещение от положения равновесия Изображение на фазовой плоскости. Фазовая траектория:
Колебательное движение с заданной амплитудой на фазовой плоскости изображается фазовой траекторией в виде эллипса с полуосями
|

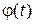 ; груз на пружине – колеблющаяся переменная
; груз на пружине – колеблющаяся переменная 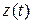 ; колебательный контур – колебания заряда конденсаторе
; колебательный контур – колебания заряда конденсаторе 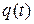 на или напряжения на нем
на или напряжения на нем 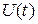 , или тока в катушке.
, или тока в катушке. Пружинный маятник: на груз действует со стороны растянутой или сжатой пружины сила ее упругости, подчиняющаяся закону Гука
Пружинный маятник: на груз действует со стороны растянутой или сжатой пружины сила ее упругости, подчиняющаяся закону Гука 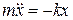 . Канонический вид уравнения:
. Канонический вид уравнения: 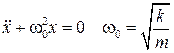

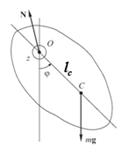

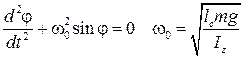
 - расстояние от неподвижной точки (крепления маятника) до центра масс тела.
- расстояние от неподвижной точки (крепления маятника) до центра масс тела.

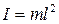
 . Приведенная длина физического маятника:
. Приведенная длина физического маятника: 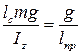
 .
. , называется центром качаний физического маятника (точка
, называется центром качаний физического маятника (точка 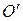 на правом рисунке). Если в центре качаний сосредоточить всю массу системы, то физический маятник превращается в математический маятник с той же собственной частотой колебаний
на правом рисунке). Если в центре качаний сосредоточить всю массу системы, то физический маятник превращается в математический маятник с той же собственной частотой колебаний 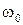 . Центр качаний удален от точки подвеса дальше, чем центр масс:
. Центр качаний удален от точки подвеса дальше, чем центр масс: 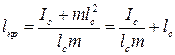 >
> 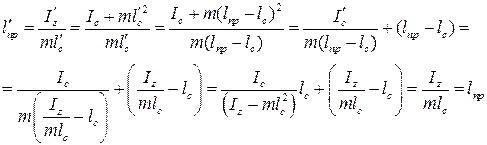
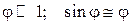
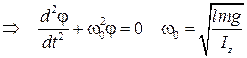
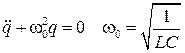 (в системе СИ).
(в системе СИ).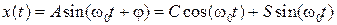 ;
; 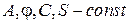
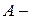 амплитуда колебаний;
амплитуда колебаний; 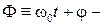 фаза колебаний,
фаза колебаний, 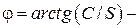 начальная фаза.
начальная фаза. . Циклическая частота
. Циклическая частота 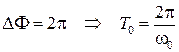

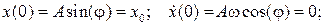
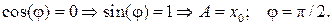
 .
.
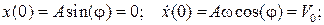

 .
. имеем
имеем 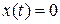 .
.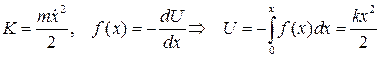
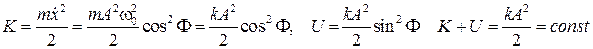
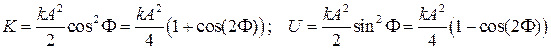
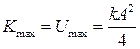
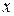 . Графики изменения энергии.
. Графики изменения энергии.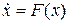
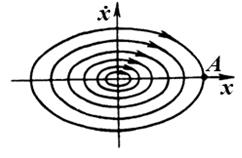
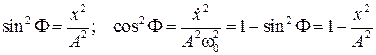

 . Фазовый портрет. Состояние равновесия – особая точка типа центра.
. Фазовый портрет. Состояние равновесия – особая точка типа центра.


