Сила вязкого трения: 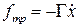
Канонический вид колебаний:
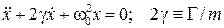
- линейное однородное уравнение с постоянными коэффициентами.
Общий способ решения. Ищем решение в виде: 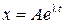 . Подставляем в уравнение:
. Подставляем в уравнение:
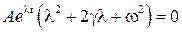
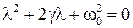
- характеристическое уравнение для исходного дифференциального уравнения.
Решения характеристического уравнения: 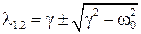
Случай малой диссипации:  <
<  :
:
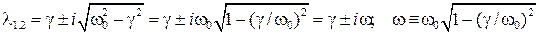
Общее решение дифференциального уравнения:
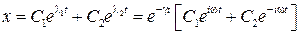
Положим  . Для вещественности величины
. Для вещественности величины 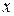 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы  . В результате решение уравнения приобретает вид:
. В результате решение уравнения приобретает вид:
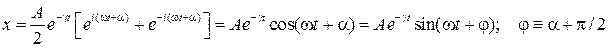
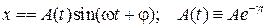
Константа  - начальная амплитуда.
- начальная амплитуда.
Графики.

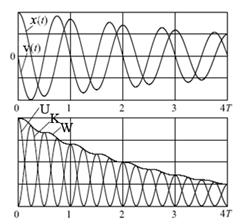
Функция  не является строго периодической, но она имеет периодический множитель. Условный период – период изменения этого множителя:
не является строго периодической, но она имеет периодический множитель. Условный период – период изменения этого множителя:  .
.
Можно считать периодом интервал времени между последовательными прохождениями положения равновесия в одном направлении. Условный период больше, чем период собственных колебаний соответствующего консервативного осциллятора (осциллятора в отсутствие силы трения).
Условный период по-прежнему не зависит от амплитуды колебаний, так что свойство изохронности колебаний сохраняется и при наличии линейной диссипации.
Случай слабого затухания: 
При  относительная разность частот 5%.
относительная разность частот 5%.
Характеристики затухания колебаний.
1.  - постоянная затухания колебаний;
- постоянная затухания колебаний;
2.  - время жизни колебаний – время, в течении которого амплитуда уменьшается в
- время жизни колебаний – время, в течении которого амплитуда уменьшается в 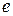 раз. В рамках линейного диссипативного осциллятора колебания продолжаются бесконечно долго. Сухое трение делает это время конечным
раз. В рамках линейного диссипативного осциллятора колебания продолжаются бесконечно долго. Сухое трение делает это время конечным
3.  - натуральный логарифм отношение максимальных последовательных отклонений. Обратная величина
- натуральный логарифм отношение максимальных последовательных отклонений. Обратная величина 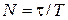 определяет, сколько циклов колебаний совершит система за время ее жизни
определяет, сколько циклов колебаний совершит система за время ее жизни  .
.
Поскольку величина  постоянная, последовательность значений:
постоянная, последовательность значений:
 представляет собой убывающую геометрическую прогрессию с периодом
представляет собой убывающую геометрическую прогрессию с периодом  <
<  . При
. При 
 . Амплитуда уменьшается очень медленно.
. Амплитуда уменьшается очень медленно.
4.  - добротность осциллятора.
- добротность осциллятора.
Все безразмерные характеристики используют сравнение с «собственной единицей времени» осциллятора - его периодом.
Затухающие колебания на фазовой плоскости – скручивающая спираль с постепенно сгущающимися витками. Спирали отвечающие разным начальным условиям нигде не пересекаются (это обеспечивает теореме существования единственности).
Сильная диссипация  >
> 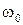 .
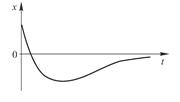
.  . Оба значения отрицательны. Неколебательные режимы.
. Оба значения отрицательны. Неколебательные режимы. 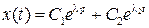 .
.
Графики возможно поведения отклонения от состояния равновесия демонстрируют либо монотонное приближение к состоянию равновесия, либо единожды (!) прохождение через состояние равновесия.
.
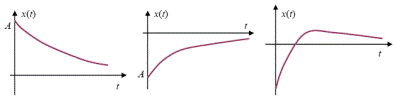
Критический случай:  .
. 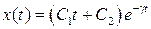
 В этом затухание колебаний происходят наиболее быстро. Благодаря этому своему свойству, ситуацию критического затухания вводится искусственно во многие устройства. В измерительных приборах для уменьшения время колебаний стрелки и его быстрого установление на нужное деление, соответствующее измеряемой величине. В автомобилях эту «успокаивающую» роль играют амортизаторы. Без их использования автомобиль бы долго качался на пружинах подвески после прохождении каждой кочки или ямки. Это неприятно для пассажиров и опасно для самого автомобиля, поскольку в моменты колебаний уменьшается сцепление с дорогой. Амортизаторы играют роль вязкого трения, коэффициент затухания стараются пообобрать так, чтобы создавалась критическая ситуация.
В этом затухание колебаний происходят наиболее быстро. Благодаря этому своему свойству, ситуацию критического затухания вводится искусственно во многие устройства. В измерительных приборах для уменьшения время колебаний стрелки и его быстрого установление на нужное деление, соответствующее измеряемой величине. В автомобилях эту «успокаивающую» роль играют амортизаторы. Без их использования автомобиль бы долго качался на пружинах подвески после прохождении каждой кочки или ямки. Это неприятно для пассажиров и опасно для самого автомобиля, поскольку в моменты колебаний уменьшается сцепление с дорогой. Амортизаторы играют роль вязкого трения, коэффициент затухания стараются пообобрать так, чтобы создавалась критическая ситуация.
Фазовые диаграммы.


Рис. «а»  <
< 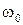 Рис. «b»
Рис. «b»  >
> 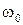 Рис. «c»
Рис. «c»  (критический режим)
(критический режим)

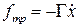
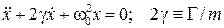
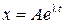 . Подставляем в уравнение:
. Подставляем в уравнение: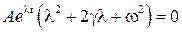
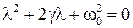
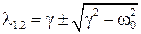
 <
<  :
: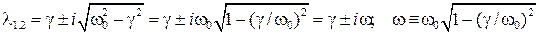
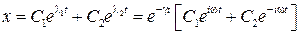
 . Для вещественности величины
. Для вещественности величины 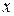 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы  . В результате решение уравнения приобретает вид:
. В результате решение уравнения приобретает вид: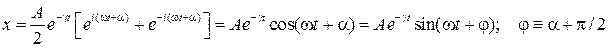
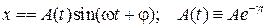
 - начальная амплитуда.
- начальная амплитуда.

 не является строго периодической, но она имеет периодический множитель. Условный период – период изменения этого множителя:
не является строго периодической, но она имеет периодический множитель. Условный период – период изменения этого множителя:  .
.
 относительная разность частот 5%.
относительная разность частот 5%. - время жизни колебаний – время, в течении которого амплитуда уменьшается в
- время жизни колебаний – время, в течении которого амплитуда уменьшается в 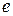 раз. В рамках линейного диссипативного осциллятора колебания продолжаются бесконечно долго. Сухое трение делает это время конечным
раз. В рамках линейного диссипативного осциллятора колебания продолжаются бесконечно долго. Сухое трение делает это время конечным - натуральный логарифм отношение максимальных последовательных отклонений. Обратная величина
- натуральный логарифм отношение максимальных последовательных отклонений. Обратная величина 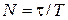 определяет, сколько циклов колебаний совершит система за время ее жизни
определяет, сколько циклов колебаний совершит система за время ее жизни  .
. постоянная, последовательность значений:
постоянная, последовательность значений: представляет собой убывающую геометрическую прогрессию с периодом
представляет собой убывающую геометрическую прогрессию с периодом  <
<  . При
. При 
 . Амплитуда уменьшается очень медленно.
. Амплитуда уменьшается очень медленно. - добротность осциллятора.
- добротность осциллятора.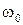 .
.  . Оба значения отрицательны. Неколебательные режимы.
. Оба значения отрицательны. Неколебательные режимы. 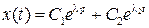 .
.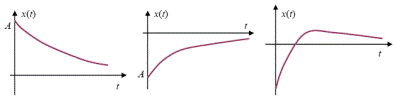

 .
. 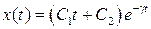
 В этом затухание колебаний происходят наиболее быстро. Благодаря этому своему свойству, ситуацию критического затухания вводится искусственно во многие устройства. В измерительных приборах для уменьшения время колебаний стрелки и его быстрого установление на нужное деление, соответствующее измеряемой величине. В автомобилях эту «успокаивающую» роль играют амортизаторы. Без их использования автомобиль бы долго качался на пружинах подвески после прохождении каждой кочки или ямки. Это неприятно для пассажиров и опасно для самого автомобиля, поскольку в моменты колебаний уменьшается сцепление с дорогой. Амортизаторы играют роль вязкого трения, коэффициент затухания стараются пообобрать так, чтобы создавалась критическая ситуация.
В этом затухание колебаний происходят наиболее быстро. Благодаря этому своему свойству, ситуацию критического затухания вводится искусственно во многие устройства. В измерительных приборах для уменьшения время колебаний стрелки и его быстрого установление на нужное деление, соответствующее измеряемой величине. В автомобилях эту «успокаивающую» роль играют амортизаторы. Без их использования автомобиль бы долго качался на пружинах подвески после прохождении каждой кочки или ямки. Это неприятно для пассажиров и опасно для самого автомобиля, поскольку в моменты колебаний уменьшается сцепление с дорогой. Амортизаторы играют роль вязкого трения, коэффициент затухания стараются пообобрать так, чтобы создавалась критическая ситуация.




