Классификация колебанийКобели: высота в холке 60-65 см, Вес 30-40 кг. Суки: высота в холке 55-60 см, вес 22-32 кг.
Прейскурант цен на услуги Шиномонтажа (легковые автомобили)
ТЕОРИЯ КОЛЕБАНИЯ Колебания нас окружают. Механические колебания. Акустические колебания (звук). Свет – колебания электромагнитного поля. Звуковые и электромагнитные колебания дают нам практически всю информацию об окружающей мире (тактильные ощущения – передаются и обрабатываются мозгом в виде эл-м. импульсов, т.е. тоже колебаний). Посредством эл.-м. волн осуществляется передача и прием информации на расстоянии. Задача теории колебаний – выявить наиболее общие закономерности колебательных процессов (вне зависимости от их природы) и описать эти закономерности математически. Сосредоточим внимание на механических колебаниях, поскольку их (в отличие от, напр. электромагнитных колебаний) «видно невооруженным глазом». Определить колебания не просто (как не просто определить, что такое «лысый человек» или «куча» Л. Мандельштамм). Проще показать. Самые общие слова: колебания – это процессы, характеризуемые определенной повторяемостью (но не обязательно, периодичностью!). В энергетическом аспекте характерный признак колебаний – повторяющейся процесс превращения энергии их одной формы в другую и обратно: для механических колебаний - из кинетической в потенциальную и обратно; для электрических колебаний – превращение электрической энергии конденсатора в магнитную энергию катушки с током; для периодических (автоколебательных) химических реакций – периодический обмен энергией с окружающей средой и пр. Классификация колебаний 1. Классификация по физическим процессам, которые происходят при колебаниях. 1. Механические колебания: груз на пружинке, математический и физический маятник и пр. Колебательные изменения претерпевают кинематические характеристики механического движения. 2. Электромагнитные колебания – колебаний в цепи с конденсатором и катушкой. 3. Смешанные колебания – колебания заряженных частиц в плазме. 2. По кинематическому признаку: периодические и непериодические. Периодические колебания: для изменяющей во времени величины выполняется 3. По сложности систем, в которых происходят колебательные процессы. Здесь определяющая характеристика – число степеней свободы системы. Простые системы - одномерные, т.е. колебания с одной степенью свободы, сложные колебания имеют место в системах – с несколькими степенями свободы, например, трехмерных системах. Бесконечномерные колебания – например, колебания натянутой струны, когда колебательные процесс совершают бесконечное число точек этой струны. 4. Разделение колебательных систем на линейные и нелинейные. Здесь определяющей характеристикой является вид дифференциальных уравнений, которые описывают колебательный процесс. Линейные уравнения содержат саму величину и все ее производные в первой степени. Пример – маятник при малых углах отклонения. Нелинейные системы содержат хотя бы одну из указанных величин в степени, отличной от единицы. Пример – маятник при любых углах отклонения. 5. Разделение колебаний по способу их возбуждения. 1. Свободны или собственные колебания. Осуществляются в системе, обладающей состоянием устойчивого равновесия. Внешнее воздействие отклоняет покоящуюся в состоянии устойчивого равновесия систему из этого ее положения. После этого отклонения система остается предоставленной самое себе – внешнее воздействие прекращается. Система, способная совершать свободные колебания, называется осциллятором. 2. Вынужденные колебания. Происходят при оказании на систему периодического внешнего воздействия. Раскачивание качелей при помощи постоянного внешнего подталкивания. При вынужденных колебаниях важным явлением является явление резонанса, когда частота периодического воздействия очень близка к частоте собственных колебаний системы. В условиях резонанса система очень сильно реагирует даже на слабое внешнее воздействие: амплитуда вынужденных колебаний резко возрастает. 3. Параметрические колебания. Возникают и поддерживаются за счет периодического изменения какого-либо внутреннего параметра системы. Например - момента инерции раскачивающегося на качелях человека (посредством попеременного сгибания и выпрямления его ног). Сами качели с находящимся на них человеком представляют пример физического маятника. Периодическое изменение момента инерции проводит к периодическому изменению приведенной длины такого маятника. Параметрические колебания тоже характеризуются резонансом («параметрический резонанс»), который в случае качелей, возникает, если частота колебаний параметра в два раза больше частоты собственных колебаний системы (за одни период колебаний качелей надо дважды сгибать и выпрямлять ноги). 4. Автоколебания – самоподдерживающиеся колебания. Пример – механические часы. Для возбуждения автоколебаний необходимо три составляющие: осциллятор – система, способная совершать собственные колебаний: постоянный (внешний) источник энергии, который компенсирует диссипативные потери; обратная связи между осциллятором и источником энергии, которая осуществляет периодический обмен энергией между осциллятором и источником, в результате чего в системе поддерживается колебательный процесс. При автоколебаниях существенно, что внешним источником энергии «командует» (управляет) сам осциллятор: именно он регулирует процесс поступления энергии от источника. Автоколебания могут осуществляться только в нелинейных диссипативных системах.
|
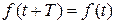. Наименьший из всех возможных интервалов 
называется периодом колебаний. Если это не выполняется колебаний непериодические. Среди периодических колебаний выделяется класс гармонических (или синусоидальных) колебаний. Зависимость от времени таких колебаний определяется синусоидальной (или косинусоидальной) или, как говорят, гармонической функцией: 
. Среди непериодических колебаний выделяются квазигармонические колебания, которые являются почти гармоническими на малых промежутках времени. Квазигармонические колебания можно назвать гармоническими колебаниями с медленно меняющейся амплитудой: 
