Общие представления и понятия
1НТ1(О) Свободные затухающие колебания реализуются в … осцилляторах Ответ: диссипативных
2НТ1(З) Свободные затухающие колебания могут быть реализованы A) только в линейных диссипативных осцилляторах *B) в любых (линейных и нелинейных) диссипативных осцилляторах C) в любых диссипативных системах D) в линейных диссипативных и нелинейных колебательных системах
3НТ1(З) Уравнение движения массы m некоторого пружинного маятника имеет вид:
При заданных начальных условиях его решение описывает *A) свободные линейные затухающие колебания B) любые свободные и несвободные затухающие колебания
4НТ1(З) Уравнение движения массы m некоторого пружинного маятника имеет вид:
Сила «сопротивления» в маятнике равна: A) *B C) D)
5НТ1(З) Уравнение движения массы m некоторого пружинного маятника имеет вид:
Коэффициент затухания колебаний в маятнике(β) равен: A) r B) *C) D)
6НТ1(С) Уравнение движения массы m некоторого пружинного маятника имеет вид:
Установите все возможные соответствия между левым и правым столбцами A) собственная частота осциллятора B) коэффициент затухания C) сила сопротивления в маятнике D) сила упругости E) коэффициент силы сопротивления F) циклическая частота затухающих колебаний
A) B) C) D) E) F) r Ответы: AE, BD, CB, EF, FA, DC
7НТ1(З) Обобщенное уравнение свободных затухающих колебаний (при наличии диссипативных сил) в линейных осцилляторах имеет вид:
В уравнении: A) β- это коэффициент затухания, ω0- циклическая частота затухающих колебаний B) β- это коэффициент силы сопротивления, ω0 – собственная частота колебаний осциллятора *C) β- это коэффициент затухания, ω0- собственная циклическая частота осциллятора D) β- сила сопротивления, ω0 – циклическая частота затухающих колебаний
8НТ1(З) Обобщенное уравнение свободных затухающих колебаний (при наличии диссипативных сил) в линейных осцилляторах имеет вид:
В электрическом контуре β равна: A)
9НТ1(З) Обобщенное уравнение свободных затухающих колебаний (при наличии диссипативных сил) в линейных осцилляторах имеет вид:
В электрическом контуре ω0 равна: A) C) *D)
10НТ1(З) Обобщенное уравнение свободных затухающих колебаний (при наличии диссипативных сил) в линейных осцилляторах имеет вид:
В физическом маятнике β равна: A) B)
11НТ1(З) Обобщенное уравнение свободных затухающих колебаний (при наличии диссипативных сил) в линейных осцилляторах имеет вид:
В уравнении β коэффициент затухания. Для данного β за единицу времени амплитуда колебаний уменьшается в… A) β - раз
12НТ1(З) Коэффициент затухания β и время релаксации колебаний τ связаны соотношением: A ) Неверные ответы: B, D
13НТ1(З) Если τ - время релаксации, β коэффициент затухания, Т - период затухающих колебаний, то логарифмический декремент A)
14НТ1(З) Если собственная частота в диссипативном осцилляторе равна ω 0 , а коэффициент затухания β, то свободные колебания в нём будут… A) при ω 0 > β гармоническими и негармоническими затухающими при ω 0 < β
15НТ1(З) Параметры электрического контура равны: RLC. Формула для логарифмического декремента затухания имеет вид: A)
16НТ1(З) Логарифмический декремент ∆ равен: *A)
17НТ1(З) Если Nε – число колебаний за которые энергия свободных колебаний в диссипативном осцилляторе уменьшается в е раз, то логарифмический декремент затухания ∆ равен: A)
18НТ1(З) Если ω – циклическая частота свободных затухающих колебаний в линейном осцилляторе, а β - коэффициент затухания, то логарифмический декремент осциллятора ∆ равен: A) *D) 19НТ1(З) Циклическая частота затухающих свободных колебаний ω A) всегда больше собственной частоты осциллятора ω0 D) не может быть определена заранее т.к. её значение зависит от начальных условий (например, при v 0 > 0 частота больше ω0)
20НТ1(З) На рисунке приведена векторная диаграмма затухающих колебаний в электрическом контуре с циклической частотой ω в момент времени t = τ, равный времени релаксации
Длина векторов 1,2,3 определяет в этот момент: A) 1. 2. 3.
B) 1. 2. UL+UR = UC(τ) 3. 3- UL C) 1 2. 3. *D) 1. 2. 3. 21НТ1(О) Коэффициент затухания β характеризует уменьшение……….(амплитуды) за единицу времени.
22НТ1(О) Чем больше инертность колебательной системы, тем коэффициент затухания β.....................(меньше). 23НТ1(О) Чем меньше инертность колебательной системы, тем коэффициент затухания β...................(больше). 24НТ1(О) Чем больше коэффициент сопротивления в колебательной системе, тем коэффициент затухания β..................(больше). 25НТ1(О) Чем меньше коэффициент сопротивления в колебательной системе, тем коэффициент затухания β..................(меньше). 26НТ1(О) Время, за которое амплитуда колебаний убывает в е раз называют временем...............(релаксации) 27НТ1(О) Коэффициент затухания тем больше, чем...................(меньше) время релаксации.
28НТ1(З) В механическом осцилляторе, совершающем затухающие колебания, количественной мерой инертности является: A) квазиупругая сила. B) сила сопротивления. *C) масса. D) коэффициент затухания. 29НТ1(З) В электрическом колебательном контуре, совершающем затухающие колебания, количественной мерой инертности является: А) индуктивность катушки. *В) емкость конденсатора. С) сопротивление контура D) коэффициент затухания. 30НТ1(З) Дифференциальным уравнением, описывающим затухающие колебания у реальных «свободных»осцилляторов является: *A) B) C) D)
31HT1(З) Смещение колеблющейся величины от положения равновесия при затухающих колебаниях определяется функцией: *A) B) C) D) 32НТ1(З) Колебательный режим в реальных осцилляторах имеет место, если A) B) *C) D)
33НТ1(З) Критический режим релаксации реальных осцилляторов имеет место, если A) *B) C) D)
34НТ1(З) Апериодический режим релаксации реальных осцилляторов имеет место, если *A) B) C) D)
35НТ1(З) Колебательный режим в пружинном маятнике имеет место, если A) B) C) *D) 36НТ1(З) Критический режим в электрическом колебательном контуре реализуется, если *A) B) C) D) 37НТ1(З) Амплитуда затухающих колебаний изменяется со временем по закону A) *B) C) D)
38НТ1(З) Добротность осцилляторов это А) при затухающих колебаниях отношение энергии потерянной за период к энергии, запасенной в данный момент В) отношение энергии, запасенной в осцилляторе к энергии, теряемой за период С) умножение на 2π отношения энергии, запасенной в осцилляторе к энергии, теряемой за период D) при затухающих колебаниях - число радиан за время, за которое энергия осциллятора уменьшается в «е» раз Неверные ответы: A,B
39НТ1(З) Осциллятор совершает затухающие колебания, если он, как система является
40НТ1(З) В механическом осцилляторе, совершающем затухающие колебания, количественной мерой инертности является
41НТ1(З) В колебательном контуре, совершающем затухающие колебания, количественной мерой инертности является
42НТ1(З) Если τ - время релаксации, A) Неверные ответы: Неверные ответы: А, В
11 НТ1(З) На рис представлена векторная диаграмма свободных гармонических колебаний, описываемых функцией
*A) B) 3 C) 6 D) 4
A) B) *C) D)
13НТ1(З) На рис представлена векторная диаграмма свободных гармонических колебаний, описываемых функцией
A) B) *C) D)
14НТ1(З) Если при свободных колебаниях потенциальная энергия осциллятора пропорциональна квадрату его «смещения» из положения равновесия A) всегда гармоническими *B) гармоническими, если отсутствуют диссипативные силы C) гармоническими, если отсутствуют диссипативные силы или они пропорциональны скорости, т.е. D) гармоническими, если возвращающая осциллятор в положение равновесия сила пропорциональна
15НТ2(З) Если при свободных колебаниях потенциальная энергия осциллятора описывается функцией A) линейными гармоническими, если сила B) нелинейными гармоническими, если сила C) нелинейными и периодическими, если в системе отсутствуют диссипативные силы D) линейными при малой и нелинейными при большой амплитуде Неверные ответы: A, В, D
16НТ1(З) Потенциальная энергия осциллятора описывается функцией A) остаётся неизменным *B) уменьшается C) растёт D) остаётся неизменным, если квазиупругая сила
17НТ1(З) Потенциальная энергия осциллятора описывается функцией:
A) при малой амплитуде практически постоянен, затем увеличивается, достигая максимума при x = b, и далее стремится к 0 *C) растёт и при х >> b, T →∞ D) Определяется не зависимостью Wn (х), а тем, как ведёт себя сила. При Т = const в других случаях T(x)
19НТ2(З) Разность фаз колебаний в контуре (0
20НТ1(О) Уравнение …………………..(пружинного) маятника.
21НТ1 (О) Уравнение (электромагнитные) колебания.
22НТ1(О) Уравнение ………………….(физического) маятника.
23НТ1(О) Уравнение ………………………..(математического) маятника.
24НТ1(З) Уравнение
A) математического маятника B) пружинного маятника C) физического маятника * D) электромагнитные
26НТ1(З) Уравнение A) математического маятника B) пружинного маятника *C) физического маятника D) электромагнитные
27НТ1(З) Уравнение *А) математического маятника B) пружинного маятника C) физического маятника D) электромагнитные
28НТ1(З) Дифференциальным уравнением, не описывающим гармонические колебания, является
29НТ1(З) Физический закон, не используемый при составлении дифференциального уравнения колебаний гармонических осцилляторов
30НТ1(З) Решением дифференциального уравнения гармонических колебаний
31НТ1(О) Если увеличить в 4 раза длину нити подвеса математического маятника, то собственная частота его колебаний уменьшится в……(2)раза.
32НТ2(О) Если увеличить массу пружинного маятника в 4 раза, то собственная частота его колебаний уменьшится в ……. (2) раза.
33НТ2(О) Если уменьшить массу пружинного маятника в 4 раза, то период его гармонических колебаний уменьшится в ……(2) раза.
34НТ1(О) При увеличении периода колебаний гармонического осциллятора в 2 раза амплитуда ускорения уменьшится в ……..(4) раза.
35НТ2(З) Точка, совершающая синусоидальные гармонические колебания с периодом 24с и начальной фазой, равной нулю, сместится от положения равновесия на половину амплитуды через:
36НТ2(З) Ускорение точки, совершающей колебания по закону
37НТ2(З) Скорость точки, совершающей колебания по закону
38НТ1(З) Собственная частота ν0 идеального колебательного контура, состоящего из конденсатора электроемкостью С = 1мкФ и катушки индуктивностью L = 1 мкГн, равна:
39НТ2(З) Частота колебаний энергии магнитного поля в идеальном колебательном контуре равна (здесь ω0 - собственная частота колебаний контура): A) ω0 B) (ω0)2 *C) 2ω0 D) (2ω0)2
40НТ2(З) Максимальное значение кинетической энергии груза массой m = 10г, совершающего гармонические колебания по закону A) 5,76 мДж *B) 7,89 мДж C) 8,51 мДж D) 9,32 мДж
41НТ2(З) Отношение кинетической энергии груза, совершающего гармонические колебания с фазой колебания *A) B) C) D)
42НТ1(О) Графиками зависимости от смещения потенциальной Wп, кинетической W к е полной W энергии пружинного маятника являются,соответственно, кривые N:
Ответ:3,1,2 43НТ1(З) Потенциальная энергия гармонических колебаний механических осцилляторов, совершающих колебания по закону A) *B) C) D)
44НТ1(З) Кинетическая энергия гармонических колебаний механических осцилляторов, совершающих колебания по закону A) B) *C) D)
45HT1(З) Полная энергия гармонических колебаний механических осцилляторов равна: *A) B) C) D)
46НТ1(З) Энергия электрического поля конденсатора, в котором заряд меняется по закону A) B) *C) D) 47НТ1(З) Полная энергия идеального электрического контура при гармонических колебаниях равна: А) В) *С) D) 48НТ1(З) Полная энергия идеального электрического контура при гармонических колебаниях равна: A) B) C) D) Неверные ответы: В, D
49HT1(З) Энергия магнитного поля катушки, в которой сила тока меняется по закону A) *B) C) D) 50НТ1(О) В электрическом контуре с индуктивностью Ответ: 20 51НТ2(З) Начальная фаза результирующего гармонического колебания, полученного от сложения двух одинаково направленных колебаний
52НТ2(З) Уравнение траектории точки, участвующей одновременно в двух взаимно перпендикулярных гармонических колебаниях
53НТ1(О) В электрическом контуре с индуктивностью Энергия электрических колебаний в контуре равна… Дж Ответ 1
54НТ1(О) Если в физическом маятнике полная энергия колебаний W = 1000 Дж, а фаза Ответ: 1) 750 2) 250 55НТ2(З) Уравнение траектории точки, участвующей одновременно в двух взаимно перпендикулярных гармонических колебаниях
56НТ2(З) Уравнение траектории точки, участвующей одновременно в двух взаимно перпендикулярных гармонических колебаниях
57НТ2(З) Уравнение траектории точки, участвующей одновременно в двух взаимно перпендикулярных гармонических колебаниях
58НТ2(З) Период биений двух одновременно звучащих камертонов, настроенных соответственно на 560 и 560,5 Гц, равен:
59НТ2(З) Амплитуда результирующего гармонического колебания, полученного от сложения двух одинаково направленных колебаний одинаковой частоты с амплитудами A1 = 4см, A2 = 8см и разностью фаз
60НТ2(З) Период биений двух одновременно звучащих камертонов, настроенных соответственно на 450 и 450,5 Гц, равен:
61НТ2(З) Начальная фаза результирующего гармонического колебания, полученного от сложения двух одинаково направленных колебаний
|

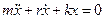

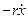

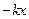
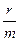
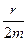



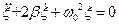
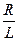
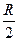
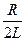

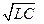
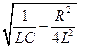


 , где
, где 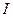 - полная длина маятника, m- его масса,
- полная длина маятника, m- его масса,  - коэффициент момента силы сопротивления
- коэффициент момента силы сопротивления , где
, где  , где
, где 
 - раз
- раз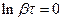
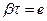

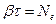 ,где
,где 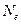 – число колебаний за которые амплитуда уменьшатся в е-раз
– число колебаний за которые амплитуда уменьшатся в е-раз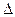 , это - …
, это - …

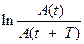
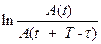
 - амплитуда затухающих колебаний
- амплитуда затухающих колебаний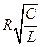
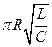
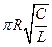

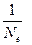 где – Ne число колебаний, за которые амплитуда свободных колебаний уменьшится в «е» раз
где – Ne число колебаний, за которые амплитуда свободных колебаний уменьшится в «е» раз 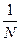 , где N -число колебаний, за которые амплитуда свободных колебаний уменьшится в 10 раз
, где N -число колебаний, за которые амплитуда свободных колебаний уменьшится в 10 раз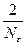
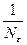


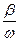
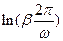





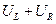
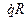
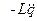
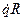




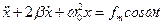


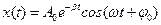




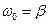

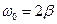

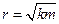
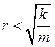
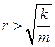
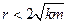


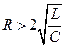
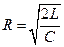
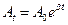
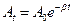

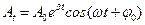
 коэффициент затухания, Т - период затухающих колебаний, то логарифмический декремент ∆ равен:
коэффициент затухания, Т - период затухающих колебаний, то логарифмический декремент ∆ равен: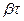

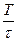

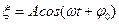 в моменты t = 0, и t = 1c. Период колебаний равен:
в моменты t = 0, и t = 1c. Период колебаний равен:

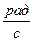 равна:
равна: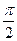

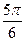
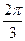
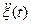 равна:
равна:
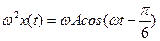
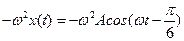

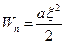 , то колебания являются:
, то колебания являются: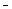

 , и негармоническими, если сила нелинейно зависит от
, и негармоническими, если сила нелинейно зависит от 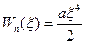 , то колебания являются:
, то колебания являются: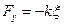 и в системе отсутствуют диссипативные силы
и в системе отсутствуют диссипативные силы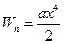 , где х - отклонение системы от положения равновесия. С ростом амплитуды период свободных незатухающих колебаний
, где х - отклонение системы от положения равновесия. С ростом амплитуды период свободных незатухающих колебаний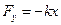 , и увеличивается в остальных случаях
, и увеличивается в остальных случаях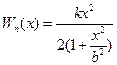 с ростом амплитуды период свободных незатухающих колебаний:
с ростом амплитуды период свободных незатухающих колебаний: 18НТ1(З) Начальная фаза синусоидальных колебаний маятника, отклоненного на угол
18НТ1(З) Начальная фаза синусоидальных колебаний маятника, отклоненного на угол 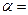 10º от вертикали и отпущенного без толчка, равна:
10º от вертикали и отпущенного без толчка, равна:
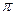
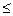
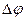
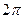 ) для двух последовательных моментов времени, в которых
) для двух последовательных моментов времени, в которых 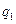 =
= 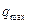 и
и 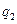 = 0 (заряд определяется на верхней пластине), равна
= 0 (заряд определяется на верхней пластине), равна

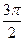
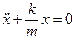 описывает гармонические колебания
описывает гармонические колебания описывает гармонические …………
описывает гармонические …………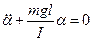 описывает гармонические колебания
описывает гармонические колебания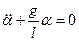 описывает гармонические колебания
описывает гармонические колебания .
.
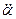 + mgl
+ mgl 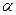 = 0.
= 0.
 .
.
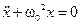 .
.
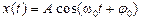



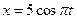 , в момент времени t, равный половине периода, равно:
, в момент времени t, равный половине периода, равно: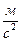
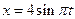 , в момент времени t, равный половине периода, равна:
, в момент времени t, равный половине периода, равна: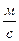
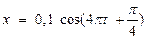 м, равно:
м, равно: , к его потенциальной энергии равно:
, к его потенциальной энергии равно:


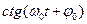

 , описывается формулой:
, описывается формулой: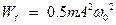

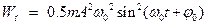
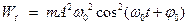
 , имеет вид:
, имеет вид: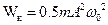
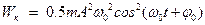
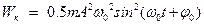
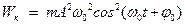
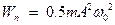

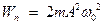
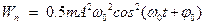
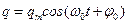 , равна
, равна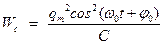
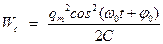

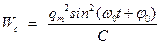
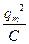
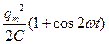
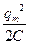
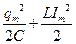
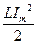



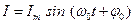 , равна:
, равна: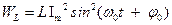
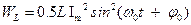
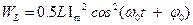
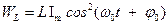
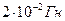 при свободных гармонических колебаниях в момент времени, когда
при свободных гармонических колебаниях в момент времени, когда 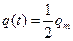 , магнитная энергия, запасенная в контуре составила 1 Дж. Максимальное значение тока в контуре(I m) равно …, А
, магнитная энергия, запасенная в контуре составила 1 Дж. Максимальное значение тока в контуре(I m) равно …, А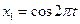 см и
см и  см, равна:
см, равна:
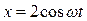 см и
см и 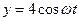 см имеет вид:
см имеет вид: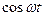
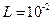 Гн при свободных гармонических с частотой
Гн при свободных гармонических с частотой 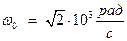 амплитуда колебаний электрического заряда составила
амплитуда колебаний электрического заряда составила 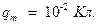
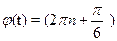 , n Є N, то потенциальная и кинетическая энергии в этот момент, соответственно, равны: 1) Wп = … Дж 2) Wк = … Дж.
, n Є N, то потенциальная и кинетическая энергии в этот момент, соответственно, равны: 1) Wп = … Дж 2) Wк = … Дж. и
и 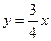
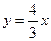


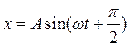 и
и  имеет вид:
имеет вид:
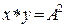


 и
и  имеет вид:
имеет вид:
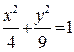

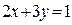
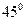 , равна:
, равна: см и
см и  см, равна:
см, равна:




