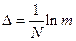Элементы теории.
1НТ1(З) Колебательная функция колебаний тока в RLC контуре имеет вид:
где φ 0 – начальная фаза колебаний заряда на конденсаторе. Электрический ток А)опережает по фазе в начальный момент напряжение на конденсаторе, на ψ - φ 0
2НТ1(З) При затухающих колебаниях скорость *A) опережает по фазе смещения (заряд на конденсаторе) на C) всегда опережает по фазе на
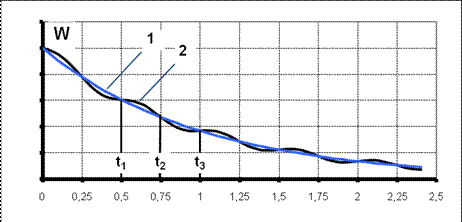
3НТ1(О) На рисунке изображены процессы релаксации осцилляторов в апериодическом режиме. Начальным условиям
Ответ: 5 4НТ1(О) На рисунке изображены процессы релаксации осцилляторов в апериодическом режиме начальным условиям
Ответ: 3
5НТ1(О) На рисунке изображены процессы релаксации осцилляторов в апериодическом режиме начальным условиям
Ответ: 1, 2
6НТ1(О) На рисунке изображены процессы релаксации осцилляторов в апериодическом режиме начальным условиям
Ответ: 4
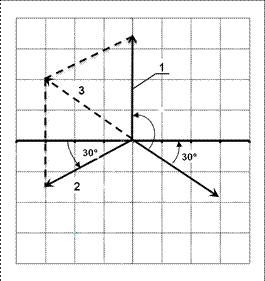
7НТ1(З)На рисунке приведена векторная диаграмма затухающих колебаний в электрическом контуре с циклической частотой ω в момент времени t = τ, равный времени релаксации.
Для построения векторной диаграммы в момент t = 0 A) следует просто увеличить диаграмму в «е» раз B) следует увеличить диаграмму в «е» раз и повернуть на угол φ = ωτ в направлении указанном на рис стрелкой *C) следует увеличить диаграмму в «е» раз и повернуть на угол φ = ωτ в направлении противоположном указанному на рис стрелкой D) построить нельзя, т.к. необходимо знать начальную фазу φ 0 8НТ1(З) Скорость убывания амплитуды заряда при затухающих колебаниях в электрическом контуре с ростом индуктивности L. A) не меняется *B) уменьшается С) возрастает D) растет прямо пропорционально L 9НТ1(З) На рис. Представлена зависимость энергии затухающих колебаний от времени. Кривая 1 описывается функцией и определяет изменение: А) полной энергией запасенной в каждый момент времени, *В) средней энергии за период, запасенной в колебаниях, C) Полной энергии запасенной в колебаниях в каждый момент времени D) Средней энергии за период, запасенной в колебаниях,
10НТ1(З) На рисунке представлен график зависимости энергии затухающих колебаний от времени.
Кривые 1 и 2 определяют изменение со временем: А) 1- полной энергии, запасенной в колебаниях. 2 – осцилляции потенциальной энергии В) 1- полной энергии, запасенной в колебаниях.2 – осцилляции кинетической энергии в колебаниях. С) 1 – средней за период энергии, запасенной в колебаниях. 2 – Осцилляции суммы Wп+Wк в течение периода. D) 1 – изменение средней за период энергии в колебаниях. 2 – изменение полной энергии в каждый момент времени. Неверные ответы: А, В 11НТ1(З) На рис. представлена зависимость энергии затухающих колебаний от времени. Кривая 2 описывает: А) колебания кинетической энергии вокруг среднего значения (кривая 1) и по ним можно оценить условный период затухающих колебаний, который будет равен T = t2-t1 B) Колебания потенциальной энергии вокруг среднего значения (кривая 1) и по ним можно оценить условный период затухающих колебаний, который будет равен T=t3-t1 C) Колебания полной энергии вокруг среднего значения (кривая 1) и по ним можно оценить условный период затухающих колебаний, который будет равен T = t3-t1 D) Колебания полной энергии вокруг среднего значения (кривая 1) и по ним можно оценить условный период затухающих колебаний, который будет равен T = t2-t1
12НТ1(З) На рис. представлена зависимость энергии затухающих колебаний от времени. Максимумы потенциальной энергии имеют место в моменте времени: А) t2, t4 и т.д. B) Во все моменты отмеченные на рисунке *С) t1, t3, t5 и т.д. D) По рисунку положение максимумов определить нельзя, т.к. 2 не определяет изменение потенциальной энергии, а это колебания полной энергии
13НТ1(З) На рис. представлена зависимость энергий затухающих колебаний от времени.
Максимумы кинетической энергии имеют место в моменты времени: *А) t2, t4, … B) Во все моменты отмеченные на рисунке С) t1, t3, t5,… D) По рисунку положение максимумов определить нельзя, т.к. 2 не определяет изменение кинетической энергии, а это колебания полной энергии
14НТ1(З) На рис. представлена зависимость энергий затухающих колебаний от времени.
Максимальная работа силы сопротивления имеет место в моменты времени: А) t1, t3, t5 *B) t2, t4 и т.д. С) между моментами t1 – t2, t3-t4,… D) t0-t1; t2-t3; t4-t5 и т.д.
15НТ1(З) На рис. представлена зависимость энергий затухающих колебаний от времени.
Осциллятор проходит положение равновесия ( A) B) Т.к. здесь максимальная разница между W(t) и < W(t)> (кривая 1), *С) D) Определить по представленным графикам нельзя, т.к. они описывают изменение энергии, а не колебания амплитуды.
16НТ1(З) На рис. представлена зависимость энергий затухающих колебаний от времени.
Отличие изменения полной энергии(2) от средней(1) обусловлено: А) неравномерным действием в осцилляторе квазиупругой силы, что приводнит к разным потерям энергии из – за действия диссипативной силы В) неравномерным совершением работы диссипативной силы, которая максимальна при C) Неравномерным совершением работы диссипативной силы, которая максимальна при D) Тем, что полная энергия равна сумме потенциальной (W C) и кинетической (W L) энергии, максимумы которых сдвинуты по времени друг относительно друга Неверные ответы: В, D
17НТ2(З) На рисунке изображены процессы релаксации осцилляторов в апериодическом режиме с одинаковой собственной частотой ω 0, в том числе и кривая, соответствующая критическому режиму
Критический режим описывается: A) Кривой 4, т.к. β = ω 0 у остальных кривых β > ω 0 B) Кривой 1- т.к. она соответствует наиболее быстрому уменьшению ξ в начальные моменты, что и должно иметь место при критическом режиме *C) Зависимостью ξ (t) №2, т.к. они соответствуют наиболее быстрому уменьшению ξ при больших t D) Кривой 1, т.к. при критическом режиме при малых t, должно происходить сразу уменьшение ξ, а при больших t время релаксации должен быть одним из самых больших.
18НТ2(З) На рисунке изображены процессы релаксации осцилляторов в апериодическом режиме с одинаковой собственной частотой ω 0, в том числе и кривая, соответствующая критическому режиму В ответе расставьте все кривые в соответствии с ростом коэффициента затухания (β)
Ответ: 2, 3, 1, 4 19НТ2(З) В электрическом контуре, число колебаний, за которое амплитуда уменьшается в «е» раз-Ne. Верные ответы:
1) Верные ответы: 2, 3, 5, 8 20НТ3(С) Установите все возможные соответствия между левым и правым столбцами для высоко добротного электрического контура (Q >> 1). Ne – число колебаний, за которое амплитуда уменьшается в «e» раз. A) B) Δ B)Ne C) β C) D) E) F)
Ответы: АВ, АС, АЕ, ВА, ВF, CD
21НТ1(З) Дифференциальным уравнением, описывающим затухающие колебания реальных осцилляторов, является: *А) В) С) D)
22НТ1(З) Смещение колеблющейся величины от положения равновесия при затухающих колебаниях определяется функцией: *A) B) C) D)
23НТ1(З) Колебательный режим в реальных осцилляторах имеет место, если A) B) *C) D)
24НТ1(З) Критический режим релаксации реальных осцилляторов имеет место, если A) *B) C) D)
25НТ1(З) Апериодический режим релаксации реальных осцилляторов имеет место, если *A) B) C) D)
26НТ1(З) Колебательный режим в пружинном маятнике имеет место, если А) В) С) *D)
27НТ1(З) Критический режим в колебательном контуре реализуется, если *A) B) C) D)
28НТ1(З) Амплитуда затухающих колебаний изменяется со временем по закону A) *B) C) D) 29НТ1(З) Скорость убывания амплитуды заряда в колебательном контуре с ростом индуктивности L
А) не меняется *В) убывает С) возрастает D) растет прямо пропорционально L
30НТ2(O) Составьте дифференциальное уравнение свободных затухающих колебаний пружинного маятника по шаблону:
где
Ответ: a2F1+b4a1F1+b2F1=0
31НТ2(О) Составьте дифференциальное уравнение свободных затухающих коле баний пружинного маятника по шаблону:
где
Ответ: a2F1+b4a1F1+b2F1=0
32НТ2(О) Составьте дифференциальное уравнение затухающих электромагнит ных колебаний колебательного контура по шаблону:
где
Ответ:
33НТ2(О)Составьте дифференциальное уравнение затухающих колебаний заря- да конденсатора в колебательном контуре по шаблону:
где
Ответ:
34НТ2(О) Записать закон затухающих колебаний для смещения маятника из положения равновесия по шаблону:
где
колебаний; Ответ
Задачи 1НТ1(О) При β >> ω 0 и ω0 = 10 Ответ: 50 2НТ1(О) При β >> ω0 и β = 20 ω0 = … Ответ: 2 3НТ3(З) Известно, что в общем случае апериодический процесс релаксации описывается двумя слагаемыми, одно из которых убывает при β >> ω0 существенно быстрее другого. Если собственная частота осциллятора А) В) 0,05 с С) 0,01 с *D) 0,1 с 4НТ1(О) Если собственная частота колебаний диссипативного осциллятора равна ω0 = 10
Ответ: 10 5НТ1(О) В электрическом контуре Ответ: 2 6НТ1(З) Для того, чтобы в RLC контуре имели место колебания при R= 20 Ом и С = 1 МкФ, индуктивность должна быть больше L > … Гн *А) 7НТ1(О) Частота свободных затухающих колебаний диссипативного осциллятора равна 4 Коэффициент затухания осциллятора равен β =… Ответ: 3 8НТ1(О)Циклическая частота свободных затухающих колебаний в RLC контуре с сопротивлением R = 6 Ом равна 4 Индуктивность контура равна L =… Гн Ответ:1
9НТ2(З) Начальная фаза в RLC контуре
Ответ: В 10НТ2(О) Отношение квадратов циклической частоты затухающих колебаний к коэффициенту затухания равно 3. Сдвиг фазы между напряжением на конденсаторе и током в RLC контуре равен(в градусах)… Ответ: 150 11НТ2(О) На рисунке приведена векторная диаграмма затухающих колебаний для некоторого момента времени в RLC контуре, циклическая частота колебаний ω = 10
Коэффициент затухания контура равен β = … Ответ: 10 12НТ2(О) На рисунке приведена векторная диаграмма затухающих колебаний для некоторого момента времени в RLC контуре, циклическая частота колебаний ω = 10
Индуктивность контура L = 0,1 Гн. Сопротивление контура R = … Ом Ответ: 2 13НТ1(О)В пружинном маятнике коэффициент силы сопротивления равен r 0 = 0,4 Ответ: 40
14НТ1(З) Колебательная функция некоторого диссипативного осциллятора имеет вид
Ответ: А
15НТ1(З)Колебательная функция некоторого диссипативного осциллятора имеет вид
Ответ: D
16НТ2(О) Параметры электрического колебательного контура равны L = 2 мГн, С = 0,2 мкФ, R = 4 Ом. Амплитуда свободных затухающих колебаний в контуре уменьшится в «e» раз после изменения фазы колебаний на … рад Ответ: 50 17НТ2(О) Параметры электрического колебательного контура равны L = 2 мГн, С = 0,2 мкФ, R = Число колебаний за которое амплитуда колебаний уменьшится в «е» раз равно… Ответ:50 18НТ2(О) Параметры электрического колебательного контура равны L = 2 мГн, С = 0,2 мкФ, R = Ответ: 25
19НТ1(О) в электрическом контуре с индуктивностью L = 10-2 Гн и емкостью С = 5 мкФ. амплитуда электрического заряда в контуре при свободных гармонических колебаниях q m = 10-2 Кл. Энергия колебаний заряда в контуре равна… Дж Ответ: 1 20НТ1(З) Если логарифмический декремент Δ = 0,02, то энергия колебаний уменьшится в е раз через N полных колебаний A) N = 50 B) N = 100 *C) N = 25 D) N = 250 21HT1(З) Если за 50 полных колебаний энергия системы уменьшилась в е раз, то логарифмический декремент системы равен: *A)0,01 B) 0,02 C) 0,05 D) 0,5 22НТ2(З) Логарифмический декремент Δ, при котором энергия колебательного контура за N полных колебаний уменьшилась в m раз, равен: *A) B) C) D) 23HT2(з) Амплитуда затухающих колебаний системы с добротностью θ - 100π уменьшится в е раз через число колебаний Ne, равное A) 10 *B) 100 C) 50 D) 200
24НТ2(з) Энергия затухающих колебаний системы с добротностью θ - 100π уменьшится в е раз через число колебаний N, равное A) 10 B) 100 *C) 50 D.)200 25НТ2(З) Добротность осциллятора, в котором амплитуда колебаний уменьшается в г раз через 100 периодов, равна: A) 100 *B) 100π C) 50π D) 200
26НТ2(З) Фаза колебаний осциллятора изменилась на ∆φ = 50π при уменьшении его энергии в е раз. Добротность осциллятора равна: А) 50 В) 100π *С) 50 π D) 100 27НТ1(З) Добротность θ колебательного контура, состоящего из катушки с индуктивностью L = 2мГн, конденсатора с емкостью C = 0,2мкФ и резистора с сопротивлением R = 1 Ом, равна:
|


 (ток)
(ток) , т.к. при движении кинетическая энергия вследствие действия силы сопротивления частично превращается в тепло
, т.к. при движении кинетическая энергия вследствие действия силы сопротивления частично превращается в тепло по причине упомянутой в А
по причине упомянутой в А > 0, v0 > 0 соответствует график:
> 0, v0 > 0 соответствует график:
 > 0 соответствует график:
> 0 соответствует график:






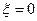 ) и имеет максимальное (
) и имеет максимальное ( )отклонение в моменты времени:
)отклонение в моменты времени: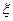 = 0- t1, t3, t5, …
= 0- t1, t3, t5, … 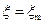 - t2,t4,…
- t2,t4,… -t1,t3,t5…
-t1,t3,t5… и равна 0 при
и равна 0 при 


 = …
= …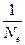 2)
2)  3)
3) 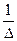 4)
4)  5)
5)  6)
6)  7)
7)  8)
8) 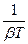


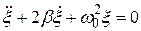


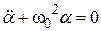
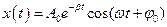


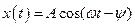
















 ,
,

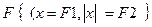
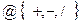
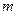 -масса груза, к- жесткость пружины,
-масса груза, к- жесткость пружины,  -коэффициент сил сопротивления
-коэффициент сил сопротивления -смещение из положения равновесия
-смещение из положения равновесия
 )
)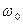 -собственная (циклическая) частота свободных колебаний,
-собственная (циклическая) частота свободных колебаний, -коэффициент затухания,
-коэффициент затухания,  ,
,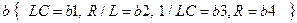

 -индуктивность катушки,
-индуктивность катушки, 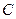 -емкость конденсатора,
-емкость конденсатора,  - сопротивление
- сопротивление -заряд.
-заряд.
 ,
,
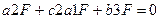
 ,
,
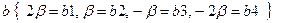

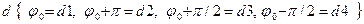


 -время,
-время,  -начальные смещение и амплитуда колебаний
-начальные смещение и амплитуда колебаний
 амплитуда отклонения осциллятора при его свободной релаксации изменилась в «е» раз за время t = 1с коэффициент затухания β = …
амплитуда отклонения осциллятора при его свободной релаксации изменилась в «е» раз за время t = 1с коэффициент затухания β = … 
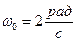 , а более «медленное» слагаемое убывает в «е» раз за t = 0,2 с. То пренебречь быстро убывающим слагаемым можно уже при t >>…
, а более «медленное» слагаемое убывает в «е» раз за t = 0,2 с. То пренебречь быстро убывающим слагаемым можно уже при t >>…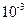 c
c Гн, С = 1МкФ критический режим процесса релаксации тока после отключения контура от источника будет иметь место при R = … Ом
Гн, С = 1МкФ критический режим процесса релаксации тока после отключения контура от источника будет иметь место при R = … Ом В)
В) 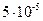 С)
С) 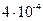 D)
D) 

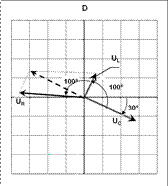
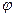 = 30о сдвиг фазы между током и напряжением на UL
= 30о сдвиг фазы между током и напряжением на UL  = 100о векторная диаграмма колебаний имеет вид:
= 100о векторная диаграмма колебаний имеет вид:





 , а коэффициент затухания
, а коэффициент затухания  . если частота свободных колебаний маятника ω0 = 20
. если частота свободных колебаний маятника ω0 = 20  , то коэффициент упругости пружины k = …,
, то коэффициент упругости пружины k = …, 
 . График функции приведён на рисунке…
. График функции приведён на рисунке…



 . График функции приведён на рисунке:
. График функции приведён на рисунке: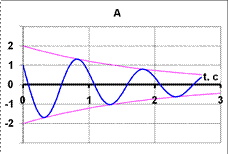


 Ом.
Ом.