Известно, что если функция  непрерывна на отрезке
непрерывна на отрезке  и известна её первообразная
и известна её первообразная  , то определенный интеграл от этой функции в пределах от a до
, то определенный интеграл от этой функции в пределах от a до  может быть вычислен по формуле Ньютона-Лейбница:
может быть вычислен по формуле Ньютона-Лейбница:
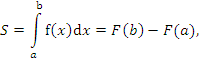
где  , штрихом вверху обозначен знак операции дифференцирования первообразной
, штрихом вверху обозначен знак операции дифференцирования первообразной  , по независимой переменной
, по независимой переменной  .
.
Однако во многих случаях первообразная  не может быть найдена или не имеет смысла (если
не может быть найдена или не имеет смысла (если  задана таблично). Поэтому важное значение имеют численные методы вычисления определенных интегралов. Численные методы являются приближенными, в основу их алгоритмов положен геометрический смысл определенного интеграла.
задана таблично). Поэтому важное значение имеют численные методы вычисления определенных интегралов. Численные методы являются приближенными, в основу их алгоритмов положен геометрический смысл определенного интеграла.
Определенный интеграл
 (6.1)
(6.1)
представляет собой площадь, ограниченную кривой подинтегральной функции  , осью абсцисс и прямыми
, осью абсцисс и прямыми  и
и  (см. рис. 6.1).
(см. рис. 6.1).
Обычно, обозначают  Для вычисления искомой площади, отрезок
Для вычисления искомой площади, отрезок  разбивают на
разбивают на  интервалов, каждый величиной
интервалов, каждый величиной
 (6.2)
(6.2)
которая называется шагом интегрирования. На каждом интервале, величиной h, площадь ‘элементарной’ фигуры, ограниченной кривой подинтегральной функции  , 2-мя ординатами (например,
, 2-мя ординатами (например, 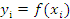 и
и  ) и осью абсцисс, заменяют площадью, ограниченной прямой, теми же ординатами и осью абсцисс, т.е. площадью ‘элементарной’ трапеции. Отсюда следует название – метод трапеций. В целом, на отрезке
) и осью абсцисс, заменяют площадью, ограниченной прямой, теми же ординатами и осью абсцисс, т.е. площадью ‘элементарной’ трапеции. Отсюда следует название – метод трапеций. В целом, на отрезке  кривая подинтегральной функции
кривая подинтегральной функции  заменяется (аппроксимируется) кусочно-линейной функцией (см. рис. 6.1).
заменяется (аппроксимируется) кусочно-линейной функцией (см. рис. 6.1).
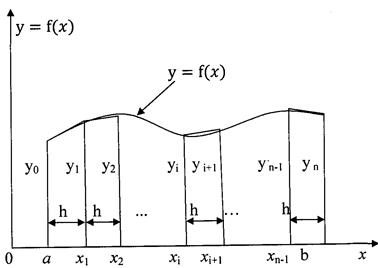
Рис. 6.1. Геометрический смысл определенного интеграла.
Площадь ‘элементарной’ трапеции  для интервала с номером
для интервала с номером  вычисляется по формуле:
вычисляется по формуле:
 (6.3)
(6.3)
а площадь, ограниченная кривой подынтегральной функции 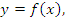 осью абсцисс и ординатами
осью абсцисс и ординатами  и
и  , приближенно будет равна сумме площадей ‘элементарных’ трапеций. Тогда можно записать:
, приближенно будет равна сумме площадей ‘элементарных’ трапеций. Тогда можно записать:
 (6.4)
(6.4)
Эту запись называют формулой трапеций. В формуле (6.4) последняя форма записи является удобной для составления программ на алгоритмических языках.

 непрерывна на отрезке
непрерывна на отрезке  и известна её первообразная
и известна её первообразная  , то определенный интеграл от этой функции в пределах от a до
, то определенный интеграл от этой функции в пределах от a до  может быть вычислен по формуле Ньютона-Лейбница:
может быть вычислен по формуле Ньютона-Лейбница: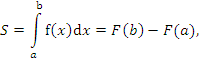
 , штрихом вверху обозначен знак операции дифференцирования первообразной
, штрихом вверху обозначен знак операции дифференцирования первообразной  .
. задана таблично). Поэтому важное значение имеют численные методы вычисления определенных интегралов. Численные методы являются приближенными, в основу их алгоритмов положен геометрический смысл определенного интеграла.
задана таблично). Поэтому важное значение имеют численные методы вычисления определенных интегралов. Численные методы являются приближенными, в основу их алгоритмов положен геометрический смысл определенного интеграла. (6.1)
(6.1) , осью абсцисс и прямыми
, осью абсцисс и прямыми  и
и  (см. рис. 6.1).
(см. рис. 6.1). Для вычисления искомой площади, отрезок
Для вычисления искомой площади, отрезок  интервалов, каждый величиной
интервалов, каждый величиной (6.2)
(6.2)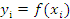 и
и  ) и осью абсцисс, заменяют площадью, ограниченной прямой, теми же ординатами и осью абсцисс, т.е. площадью ‘элементарной’ трапеции. Отсюда следует название – метод трапеций. В целом, на отрезке
) и осью абсцисс, заменяют площадью, ограниченной прямой, теми же ординатами и осью абсцисс, т.е. площадью ‘элементарной’ трапеции. Отсюда следует название – метод трапеций. В целом, на отрезке 
 для интервала с номером
для интервала с номером  вычисляется по формуле:
вычисляется по формуле: (6.3)
(6.3)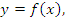 осью абсцисс и ординатами
осью абсцисс и ординатами  , приближенно будет равна сумме площадей ‘элементарных’ трапеций. Тогда можно записать:
, приближенно будет равна сумме площадей ‘элементарных’ трапеций. Тогда можно записать: (6.4)
(6.4)


