ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ.
ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ. 1) Уравнение с угловым коэффициентом.
j – угол с OX, на OY отсекает b
A (x; y) – любая точка прямой
3) Уравнение прямой, проходящей через заданную точку A(x 0; y 0) перпендикулярно данному вектору
Пример:
Написать уравнение hB.
4) Общее уравнение прямой.
Частные случаи:
5)У равнение прямой в отрезках.
6) Пучок прямых. Совокупность прямых, проходящих через одну общую точку, называется пучком прямых; общая точка называется центром пучка.
Пример: Сторонами треугольника являются координатные оси и прямая, проходящая через точку (3; 4). Найти уравнение прямой, если площадь треугольника равна 9. Решение:
Ответ: 7) Уравнение прямой, проходящей через две точки
Пример: Записать уравнение медианы треугольника ABC, проведенной из вершины A, если A(–1: 3), B(3; 5), C(1; –3).
8) Условие принадлежности трех точек одной прямой.
9) Нормальное уравнение прямой.
M (x; y) – произвольная точка прямой.
Условия, при которых уравнение является нормальным: 1) 2) Пример:
Любое уравнение можно привести к нормальному.
Пример:
|

 Дано:
Дано:

 2) Уравнение прямой, проходящей через точку A(x 0; y 0) под заданным углом j.
2) Уравнение прямой, проходящей через точку A(x 0; y 0) под заданным углом j.

 – уравнение прямой, проходящей через точку под заданным углом.
– уравнение прямой, проходящей через точку под заданным углом. – уравнение прямой, проходящей через O(0; 0) (начало координат)
– уравнение прямой, проходящей через O(0; 0) (начало координат)
 M (x; y) – произвольная точка прямой
M (x; y) – произвольная точка прямой
 – координаты вектора
– координаты вектора 

 Дан DABC: A(3; 2), B(–1; 4), C(5; 6).
Дан DABC: A(3; 2), B(–1; 4), C(5; 6).
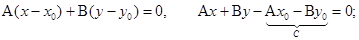
 – общее уравнение прямой
– общее уравнение прямой

 1) A = 0,
B y + C = 0,
1) A = 0,
B y + C = 0,
 y = b
y = b
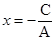 x = a
x = a


 – уравнение прямой в отрезках.
– уравнение прямой в отрезках.
 – текущий параметр.
– текущий параметр.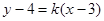 – уравнение пучка.
– уравнение пучка.


 .
.
 – уравнение прямой, проходящей через две точки.
– уравнение прямой, проходящей через две точки. -
- 

 – условие принадлежности
– условие принадлежности ON = p, a.
ON = p, a.
 – нормальное уравнение прямой.
– нормальное уравнение прямой. ,
, .
.
 , чтобы привести его к нормальному, необходимо умножить его на нормирующий множитель.
, чтобы привести его к нормальному, необходимо умножить его на нормирующий множитель. .
. Умножим уравнение на N, получим:
Умножим уравнение на N, получим: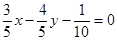 .
.


