ЛАБОРАТОРНАЯ РАБОТА № 11
ИЗУЧЕНИЕ РАСПРЕДЕЛЕНИЯ МАГНИТНОГО ПОЛЯ СОЛЕНОИДА И ОПРЕДЕЛЕНИЕ ЕГО ИНДУКТИВНОСТИ Выполнил студент -------------------------, группа -------------, дата -------. Допуск ______________ Выполнение __________ Зачет ________________ Цель работы: изучить распределение магнитного поля соленоида и определить его индуктивность; сравнить результаты измерений с теоретическими расчетами. Приборы и материалы
Теоретические сведения Основные понятия и законы 1.1. Магнитное поле и его характеристики Магнитное поле – одна из форм электромагнитного поля, релятивистский эффект электрического поля. Магнитное поле создаётся (порождается) током заряженных частиц, или изменяющимся во времени электрическим полем (током смещения), или собственными магнитными моментами частиц. С точки зрения квантовой теории поля магнитное взаимодействие – частный случай электромагнитного взаимодействия, переносится фундаментальным безмассовым бозоном – фотоном (частицей, которую можно представить как квантовое возбуждение электромагнитного поля). Магнитное поле действует только на движущиеся заряды. Оно обладает энергией, которая проявляет себя в виде электромагнитных сил, действующих на отдельные движущиеся электрические заряды (электроны и ионы) и на их потоки, т. е. электрический ток. Под влиянием электромагнитных сил движущиеся заряженные частицы отклоняются от своего первоначального пути. Основными характеристиками магнитного поля являются магнитная индукция и напряженность, магнитный момент магнитный поток, магнитная проницаемость. Вектор индукции магнитного поля Магнитное поле может оказывать разнообразные воздействия на другие физические объекты, оказавшиеся в этом поле. Механическое действие, которое магнитное поле оказывает на другие тела, можно характеризовать вектором силы, а само поле – векторной физической величиной, называемой магнитной индукцией, которая позволяет определить эту силу. Магнитная индукция обозначается буквой Индукция магнитного поля – векторная физическая величина, численно равная силе, действующей в однородном магнитном поле на проводник единичной длины с единичной силой тока, расположенный перпендикулярно магнитным силовым линиям. 1Тл – индукция однородного магнитного поля, в котором на проводник длиной 1м с током в 1А, расположенный перпендикулярно магнитным силовым линиям, действует сила 1Н. Магнитная индукция
 . .
Направление вектора магнитной индукции задается направлением магнитной стрелки, помещенной в данную точку поля. Оно совпадает с направлением, которое указывает северный полюс стрелки (рис. 1).
 можно определить с помощью силы, действующей на движущийся свободный заряд или проводник с током, где заряды перемещаются вдоль проводника, а также с помощью момента сил, действующих на рамку, по которой течет ток (рис. 2). можно определить с помощью силы, действующей на движущийся свободный заряд или проводник с током, где заряды перемещаются вдоль проводника, а также с помощью момента сил, действующих на рамку, по которой течет ток (рис. 2).
Магнитную индукцию Различают однородные и неоднородные магнитные поля. Поле, в каждой точке которого вектор магнитной индукции
На рисунке 3 приведены способы изображения силовых линий однородного магнитного поля, направленного вправо (а), влево (б), в плоскость листа от нас (в) и из него к нам (г). Опыт показывает, что для магнитного поля, как и для электрического, справедлив принцип суперпозиции: индукция магнитного поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме индукций магнитных полей, создаваемых каждым током или зарядом:
Графическое изображение магнитного поля Магнитное поле изображается графически с помощью магнитных силовых линий или линий магнитной индукции. Непрерывная линия, касательная к которой в любой ее точке задает направление вектора магнитной индукции Линии магнитной индукции всегда замкнуты, что говорит об отсутствии в природе магнитных зарядов и вихревом характере магнитного поля. Условно они выходят из северного полюса магнита и входят в южный. Густота линий выбирается так, чтобы число линий через единицу площади, перпендикулярную магнитному полю, было пропорционально величине магнитной индукции. Направление магнитного поля в каждой точке может быть определено при помощи магнитной стрелки. Северный полюс стрелки всегда устанавливается в направлении действия сил поля. Конец постоянного магнита, из которого выходят силовые линии, принято считать северным полюсом, а противоположный конец, в который входят силовые линии, – южным полюсом. На рисунке 4 показаны исследования магнитного поля вокруг полосового магнита с помощью магнитных стрелок и картина силовых линий магнитного поля вокруг такого магнита. Картина силовых линий магнитного поля, созданного постоянным подковообразным магнитом (а), прямым проводом с током (б) и проволочным кольцом (в), по которому течет ток, показана на рисунке 5. Силовые линии магнитного поля – замкнутые линии. Во внешнем пространстве постоянных магнитов они идут от северного полюса к южному.
Направление силовых линий вокруг прямолинейного провода с током определяется по правилу буравчика (правовращающий винт, штопор): если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции. Вектор напряжённости магнитного поля Магнитное поле в макроскопическом описании представлено двумя различными векторными полями, обозначаемыми, как Для однородной изотропной среды вектор магнитной индукции связан с вектором напряженности следующим выражением:
где
Магнитная проницаемость зависит только от свойств среды, в которой создаётся магнитное поле. Напряженность Магнитный момент контура с током Подобно тому, как для исследования электрического поля мы использовали пробный заряд, применим для исследования магнитного поля пробный ток, циркулирующий в плоском замкнутом контуре очень малых размеров. Будем называть такой контур пробным контуром (рис. 6).
 к контуру, восстанавливаемой по правилу правого буравчика: вращаем рукоятку правого буравчика по направлению тока в контуре, тогда направление его поступательного движения даст направление нормали к контуру, восстанавливаемой по правилу правого буравчика: вращаем рукоятку правого буравчика по направлению тока в контуре, тогда направление его поступательного движения даст направление нормали  (рис. 6). Помещая пробный контур в магнитное поле, обнаружим, что поле стремится повернуть контур (нормаль) в определенном направлении. (рис. 6). Помещая пробный контур в магнитное поле, обнаружим, что поле стремится повернуть контур (нормаль) в определенном направлении.
Вращающий момент, действующий на контур, зависит как от свойств магнитного поля в данной точке, так и от свойств контура. Оказывается, что максимальная величина вращающего момента пропорциональна Векторную величину На пробные контуры с разными
Магнитная индукция есть вектор, направление которого совпадает с направлением нормали контура с током, свободно установившегося во внешнем магнитном поле. Для произвольного замкнутого контура магнитный момент находится из:
где В общем случае произвольного распределения токов в среде:
где Гипотеза Ампера Согласно предположению французского физика А.Ампера, постоянные магниты (например, намагниченное железо, стрелки компаса) содержит непрерывно движущиеся заряды, т.е. электрические токи в атомном масштабе. Такие микроскопические токи, обусловленные движением электронов в атомах и молекулах, существуют в любом теле. Эти микротоки создают свое магнитное поле и могут сами поворачиваться во внешних полях, создаваемых проводниками с током. Например, если вблизи какого-либо тела поместить проводник с током, то под действием его магнитного поля микротоки во всех атомах определенным образом ориентируются, создавая в теле дополнительное магнитное поле. О природе и характере этих микротоков Ампер в то время ничего не мог сказать, так как учение о строении вещества находилось еще в самой начальной стадии. Гипотеза Ампера была блестяще подтверждена лишь спустя 100 лет, после открытия электрона и выяснения строения атомов и молекул. Магнитный момент – основная величина, характеризующая магнитные свойства вещества. Источником магнетизма, согласно классической теории электромагнитных явлений, являются электрические макро– и микротоки. Элементарным источником магнетизма считают замкнутый ток. Магнитным моментом обладают элементарные частицы, атомные ядра, электронные оболочки атомов и молекул. Магнитные моменты элементарных частиц (электронов, протонов, нейтронов и других), как показала квантовая механика, обусловлен существованием у них собственного механического момента – спина. Поток вектора магнитной индукции
 называется физическая величина называется физическая величина  , равная произведению величины этой площадки и проекции вектора , равная произведению величины этой площадки и проекции вектора  на направление нормали к площадке на направление нормали к площадке  (рис. 7): (рис. 7):
Интегрируя это выражение по
В однородном магнитном поле, модуль вектора индукции которого равен
 , определяемая соотношением: , определяемая соотношением:
Магнитный поток – величина алгебраическая: Единица измерения магнитного потока в систем СИ – 1 Вебер (1 Вб). 1 Вб – магнитный поток, проходящий через плоскую поверхность площадью 1 Магнитный поток через поверхность Поскольку линии магнитной индукции всегда замкнуты, для замкнутой поверхности число линий, входящих в поверхность – теорема Остроградского – Гаусса: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:
Эта теорема является математическим выражением того, что в природе отсутствуют магнитные заряды, на которых начинались бы или заканчивались линии магнитной индукции, т.е. чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми. 1.2. Явление электромагнитной индукции Электромагнитная индукция – явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него. Если поток вектора магнитной индукции через замкнутый контур меняется во времени, в этом контуре возникает ЭДС электромагнитной индукции, порождаемая (в случае неподвижного контура) вихревым электрическим полем, возникающим вследствие изменения магнитного поля со временем (в случае неизменного со временем магнитного поля и изменения потока из-за движения контура – проводника такая ЭДС возникает посредством действия силы Лоренца). Явление электромагнитной индукции было открыто Майклом Фарадеем в 1831 года. Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы (ЭДС) не зависит от того, что является причиной изменения потока – изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.
|

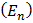
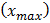

 , измеряется в теслах (Тл).
, измеряется в теслах (Тл). является основной силовой характеристикой магнитного поля. Индукция магнитного поля может быть определена в любой точке пространства и в любой момент времени:
является основной силовой характеристикой магнитного поля. Индукция магнитного поля может быть определена в любой точке пространства и в любой момент времени: Рис.1.
Рис.1.
 Рис. 2.
Рис. 2.
 можно характеризовать плотностью силовых магнитных линий, т. е. числом силовых линий, проходящих через площадь
можно характеризовать плотностью силовых магнитных линий, т. е. числом силовых линий, проходящих через площадь  или
или  , расположенную перпендикулярно магнитному полю.
, расположенную перпендикулярно магнитному полю. Рис. 3.
Рис. 3.

 Рис.4.
Рис.4.
 Рис.5.
Рис.5.
 и
и  , А/м,
, А/м, – магнитная постоянная,
– магнитная постоянная,  – безразмерная величина – магнитная проницаемость среды, которая показывает, во сколько раз индукция магнитного поля в среде
– безразмерная величина – магнитная проницаемость среды, которая показывает, во сколько раз индукция магнитного поля в среде  больше индукции
больше индукции  в вакууме (в вакууме
в вакууме (в вакууме  ):
):
 не зависит от магнитных свойств среды, но учитывает влияние силы тока и формы проводников на интенсивность магнитного поля в данной точке пространства. Однако, вектор
не зависит от магнитных свойств среды, но учитывает влияние силы тока и формы проводников на интенсивность магнитного поля в данной точке пространства. Однако, вектор  Рис. 6.
Рис. 6.
 , т.е.
, т.е.  , где
, где  – ток контуре,
– ток контуре,  – площадь контура с током.
– площадь контура с током. называют магнитным моментом контура, который в СИ измеряется в
называют магнитным моментом контура, который в СИ измеряется в  .
. m, помещаемыми в данную точку магнитного поля, будут действовать разные по величине максимальные вращающие моменты
m, помещаемыми в данную точку магнитного поля, будут действовать разные по величине максимальные вращающие моменты  , но отношение
, но отношение  будет для всех контуров одинаково, оно будет являться силовой характеристикой магнитного поля, которая называется магнитной индукцией:
будет для всех контуров одинаково, оно будет являться силовой характеристикой магнитного поля, которая называется магнитной индукцией: .
.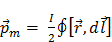 ,
, – радиуса – вектор, проведенный из начала координат до элемента длины контура
– радиуса – вектор, проведенный из начала координат до элемента длины контура  .
.
 – плотность тока в элементе объёма
– плотность тока в элементе объёма  .
. Рис.7.
Рис.7.

 , получим магнитный поток
, получим магнитный поток 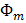 сквозь произвольную замкнутую поверхность
сквозь произвольную замкнутую поверхность 
 , помещен плоский замкнутый контур площадью
, помещен плоский замкнутый контур площадью  к плоскости контура составляет угол
к плоскости контура составляет угол  с направлением вектора магнитной индукции
с направлением вектора магнитной индукции  (см. рис. 8).
(см. рис. 8). Рис. 8.
Рис. 8.
 .
. при
при 
 и
и  при
при 
 .
. , расположенную перпендикулярно однородному магнитному полю, индукция которого равна 1 Тл.
, расположенную перпендикулярно однородному магнитному полю, индукция которого равна 1 Тл. равно числу линий, выходящих из нее
равно числу линий, выходящих из нее  , следовательно, полный поток магнитной индукции через замкнутую поверхность равен нулю.
, следовательно, полный поток магнитной индукции через замкнутую поверхность равен нулю. ,
,


