Транзисторно-транзисторная логика (ТТЛ)
На рисунке 2 изображена схема элемента 2И-НЕ ТТЛ со сложным инвертором. Применение в выходной цепи нагрузочного транзистора VT4, работающего в противофазе с выходным VT3, позволяет улучшить быстродействие и увеличить нагрузочную способность логического элемента. Сопротивление R 4 в схеме рис. 2 составляет около 100 Ом. В выходную цепь включен диод VD, который предотвращает открытие нагрузочного транзистора VT4 одновременно с выходным. Действительно, если на входы подать сигналы логической 1, т. е. U вх1 = U вх2 ³ 2,4 В, то эмиттерные переходы транзистора VT1 будут закрыты. Ток протекает через коллекторный переход транзистора VT1 в базу транзистора VT2. Транзистор VT2 переходит в насыщение, в насыщение переходит и транзистор VT3. В стандартном для интегральных микросхем открытом транзисторе U бэ = 0,7 В, а напряжение между коллектором и эмиттером насыщенного транзистора U кэ нас = 0,2 В, тогда получим U вых = U кэ VT3 = 0,2 В, U к2 = U б4 = 0,9 В. Разность напряжений в 0,7 В не позволяет открыть два p-n -перехода: база – эмиттер VT4 и диод VD. То есть при насыщении транзистора VT3 транзистор VT4 и диод VD будут закрыты. Выходное сопротивление логического элемента определяется по формуле
Выходное сопротивление показывает, как напряжение на выходе элемента зависит от тока нагрузки, а значит, от сопротивления нагрузки. Если выходное сопротивление мало (
Рисунок 2. Логический элемент 2И-НЕ ТТЛ со сложным инвертором
Выходное сопротивление элемента 2И-НЕ со сложным инвертором (рис. 2) зависит от того, какие напряжения поданы на входы. Если напряжения на всех входах логического элемента соответствуют логической единице, то выходное сопротивление равно выходному сопротивлению насыщенного транзистора VT3. Это сопротивление обычно невелико и составляет десятки Ом. Если напряжение хотя бы на одном из входов соответствует напряжению логического нуля, то выходной транзистор VT3 закрыт, ток в нагрузку идет через нагрузочный транзистор VT4 и диод VD. Запишем 2-й закон Кирхгофа для цепи U п ® R 2 ® бэVT4 ® VD ® U вых: U п = I 2 R 2 + U бэ4 + U D + U вых. (20) При закрытом транзисторе VT2 ток через сопротивление R 2 равен базовому току транзистора VT4, I 2 = I б4. Учитывая это, запишем уравнение (20) для приращений напряжений и тока: D U п = D I б4 R 2 + D U бэ4 + D U D + D U вых. (21) При постоянном напряжении питания D U п = 0. Считая, что транзистор VT4 не входит в насыщение, перепишем (21) в виде 0 = D I б4(R 2 + h 11э4) + R DD I вых + D U вых. (22) Здесь R D – дифференциальное сопротивление диода. В (22) учтено, что выходной ток элемента совпадает с током через диод. Действительно, транзистор VT3 закрыт и весь эмиттерный ток VT4 идет через диод в нагрузку. Эмиттерный ток VT4 и, следовательно, выходной ток элемента связаны с базовым током через параметр h 21э. Таким образом
Подставляя последнее равенство в (22), получим, согласно (19)
Замена транзистора VT4 и диода VD двумя транзисторами, включенными по схеме Дарлингтона (рис. 3), позволяет уменьшить выходное сопротивление элемента и повысить выходной ток транзистора VT4.
Рисунок 3. Логический элемент 2И-НЕ ТТЛ с составным нагрузочным транзистором Определим выходное сопротивление схемы, если входное напряжение соответствует напряжению логического нуля. По 2-му закону Кирхгофа U п = I 2 R 2 + U бэ5 + U бэ4 + U вых. (25) Для приращений напряжений и тока, учитывая, что I б5 = I 2, получим: D U п = D I б5 R 2 + D U бэ5 + D U бэ4 + D U вых. (26) Считая, что транзисторы VT5 и VT4 работают в активном режиме, а U п постоянно, перепишем уравнение (26): 0 = D I б5(R 2 + h 11э5) + h 11э4D I б4 + D U вых. (27) Согласно 1-му правилу Кирхгофа I э5 = I 5 + I б4, где I 5 – ток через сопротивление R 5. Базовый ток I б5 = I э5/(1 + h 21э), поэтому
Для тока I 5 используем выражение
Тогда
Подставляя это выражение в (28), получим
Используя уравнение (27) и учитывая, что
Эта величина намного меньше, чем выходное сопротивление (24) стандартного элемента с диодом (рис. 2).
|

 (19)
(19)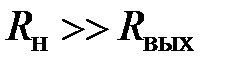 ), то даже существенное изменение выходного тока не повлияет на величину выходного напряжения, т. е. замена одной нагрузки на другую не приведет к изменению U вых.
), то даже существенное изменение выходного тока не повлияет на величину выходного напряжения, т. е. замена одной нагрузки на другую не приведет к изменению U вых.
 (23)
(23) (24)
(24)
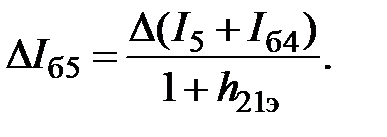 (28)
(28)
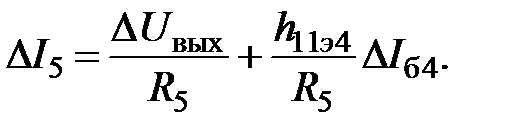
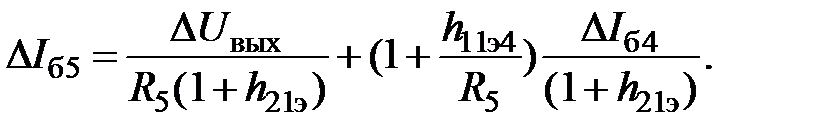 (29)
(29)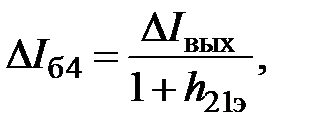 получим для выходного сопротивления элемента выражение
получим для выходного сопротивления элемента выражение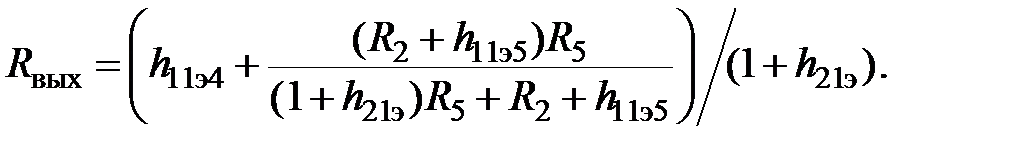 (30)
(30)


