ТЕМА 6. ОБНАРУЖЕНИЕ И ИСПРАВЛЕНИЕ ОШИБОК В СООБЩЕНИЯХ
Понятие об идее коррекции ошибок Для того чтобы в принятом сообщении можно было обнаружить ошибку это сообщение должно обладать некоторой избыточной информацией, позволяющей отличить ошибочный код от правильного Например, если переданное сообщение состоит из трех абсолютно одинаковых частей, то в принятом сообщении отделение правильных символов от ошибочных может быть осуществлено по результатам накопления посылок одного вида, например 0 или 1. Для двоичных кодов этот метод можно проиллюстрировать следующим примером: 10110 - переданная кодовая комбинация; 10010 - 1-я принятая комбинация; 10100 - -я принятая комбинация; 00110 - 3-я принятая комбинация; 10110 - накопленная комбинация. Как видим, несмотря на то, что во всех трех принятыхкомбинациях были ошибки, накопленная не содержит ошибок[8]. Принятое сообщение может также состоять из кода и его инверсии. Код и инверсия посылаются в канал связи как одно целое. Ошибка на приемном конце выделяется при сопоставлении кода и его инверсии. Для того чтобы искажение любого из символов сообщения привело к запрещенной комбинации, необходимо в коде выделить комбинации, отличающиеся друг от друга в ряде символов, часть из этих комбинаций запретить и тем самым ввести в код избыточность. Например, в равномерном блочном коде считать разрешенными кодовые комбинации с постоянным соотношением нулей и единиц в каждой кодовой комбинации. Такие коды получили название кодов с постоянным весом. Для двоичных кодов число кодовых комбинаций в кодах с постоянным весом длиной в п символов равно
где Еще одним примером введения избыточности в код является метод суть которого состоит в том, что к исходным кодам добавляются нули либо единицы таким образом, чтобы сумма их всегда. была четной или нечетной. Сбой любого одного символа всегда нарушит условие четности (нечетности), и ошибка будет обнаружена. В этом случае комбинации друг от друга должны отличаться минимум в двух символах, т. е. ровно половина комбинаций кода является запрещенной (запрещенными являются все нечетные комбинации при проверке на четность или наоборот). Во всех упомянутых выше случаях сообщения обладают избыточной информацией. Избыточность сообщения говорит о том, что оно могло бы содержать большее количество информации, если бьг не многократное повторение одного и того же кода, не добавление к коду его инверсии, не несущей никакой информации, если бы. не искусственное запрещение части комбинаций кода и т. д. Но все перечисленные виды избыточности приходится вводить для того, чтобы можно было отличить ошибочную комбинацию от правильной. Коды без избыточности обнаруживать, а тем более исправлять ошибки не могут[9]. Минимальное количество символов, в которых любые две комбинации кода отличаются друг от друга, называется кодовым расстоянием. Минимальное количество символов, в которых все комбинации кода отличаются друг от друга, называется минимальным кодовым расстоянием. Минимальное кодовое расстояние - параметр, определяющий помехоустойчивость кода и заложенную в коде избыточность. Минимальным кодовым расстоянием определяются корректирующие свойства кодов. В общем случае для обнаружения r ошибок минимальное кодовое расстояние
Минимальное кодовое расстояние, необходимое для одновременного обнаружения и исправления ошибок,
где s - число исправляемых ошибок. Для кодов, только исправляющих ошибки,
Для того чтобы определить кодовое расстояние между двумя комбинациями двоичного кода, достаточно просуммировать эти комбинации по модулю 2 и подсчитать число единиц в полученной комбинации. Понятие кодового расстояния хорошо усваивается на примере построения геометрических моделей кодов. На геометрических моделях в вершинах n-угольников, где n-значность кода, расположены кодовые комбинации, а количество ребер n-угольника, отделяющих одну комбинацию от другой, равно кодовому расстоянию. Если кодовая комбинация двоичного кода А отстоит от кодовой комбинации В на расстоянии d, то это значит, что в коде А нужно d символов заменить на обратные, чтобы получить код В, но это не означает, что нужно d добавочных символов, чтобы код обладал данными корректирующими свойствами. В двоичных кодах для обнаружения одиночной ошибки достаточно иметь 1 дополнительный символ независимо от числа информационных разрядов кода, а минимальное кодовое расстояние Для обнаружения и исправления одиночной ошибки соотношение между числом информационных разрядов и числом корректирующих разрядов должно удовлетворять следующим условиям:
при этом подразумевается, что общая длина кодовой комбинации
Для практических расчетов при определении числа контрольных разрядов кодов с минимальным кодовым расстоянием удобно пользоваться выражениями:
если известна длина полной кодовой комбинации п, и
если при расчетах удобнее исходить из заданного числа информационных символов [10]. Для кодов, обнаруживающих все трехкратные ошибки
или
Для кодов длиной в п символов, исправляющих одну или две ошибки
Для практических расчетов можно пользоваться выражением
Для кодов, исправляющих 3 ошибки
Для кодов, исправляющих s ошибок />
Выражение слева известно как нижняя граница Хэмминга [16], а выражение справа – как верхняя граница Варшамова – Гильберта [3][11] Для приближенных расчетов можно пользоваться выражением
Можно предположить, что значение Линейные групповые коды Линейными называются коды, в которых проверочные символы представляют собой линейные комбинации информационных символов. Для двоичных кодов в качестве линейной операции используют сложение по модулю 2. Правила сложения по модулю 2 определяются следующими равенствами:
Последовательность нулей и единиц, принадлежащих данному коду, будем называть кодовым вектором. Свойство линейных кодов: сумма (разность) кодовых векторов линейного кода дает вектор, принадлежащий данному коду. Линейные коды образуют алгебраическую группу по отношению к операции сложения по модулю 2. В этом смысле они являются групповыми кодами. Свойство группового кода: минимальное кодовое расстояние между кодовыми векторами группового кода равно минимальному весу ненулевых кодовых векторов. Вес кодового вектора (кодовой комбинации) равен числу его ненулевых компонентов. Расстояние между двумя кодовыми векторами равно весу вектора, полученного в результате сложения исходных векторов по модулю 2. Таким образом, для данного группового кода
Групповые коды удобно задавать матрицами, размерность которых определяется параметрами кода и
Коды, порождаемые этими матрицами, известны как Порождающая матрица С может быть представлена двумя матрицами И и П (информационной и проверочной). Число столбцов матрицы П равно
Теорией и практикой установлено, что в качестве матрицы И удобно брать единичную матрицу в канонической форме:
При выборе матрицы П исходят из следующих соображений: чем больше единиц в разрядах проверочной матрицы П, тем ближе соответствующий порождаемый код к оптимальному[12], с другой стороны, число единиц в матрице П определяет число сумматоров по модулю 2 в шифраторе и дешифраторе, т. е. чем больше единиц в матрице П, тем сложнее аппаратура. Вес каждой строки матрицы П должен быть не менее, где При соблюдении перечисленных условий любую порождающую матрицу группового кода можно привести к следующему виду:
называемому левой канонической формой порождающей матрицы. Для кодов с
Во всех комбинациях кода, построенного при помощи такой матрицы, четное число единиц. Для кодов с Корректирующие коды с минимальным количеством избыточных разрядов называют плотно упакованными или совершенными кодами. Для кодов с Плотно упакованные коды, оптимальные с точки зрения минимума избыточных символов, обнаруживающие максимально возможное количество вариантов ошибок кратностью r + 1; r + 2 и т. д. и имеющие Строчки образующей матрицы С представляют собой комбинаций искомого кода. Остальные комбинации кода строятся при помощи образующей матрицы по следующему правилу: корректирующие символы, предназначенные для обнаружения или исправления ошибки в информационной части кода, находятся путем суммирования по модулю 2 тех строк матрицы П, номера которых совпадают с номерами разрядов, содержащих единицы в кодовом векторе, представляющем информационную часть кода. Полученную комбинацию приписывают справа к информационной части кода и получают вектор полного корректирующего кода. Аналогичную процедуру проделывают со второй, третьей и последующими информационными кодовыми комбинациями, пока не будет построен корректирующий код для передачи всех символов первичного алфавита. Алгоритм образования проверочных символов по известной информационной части кода может быть записан следующим образом:
В процессе декодирования осуществляются проверки, идея которых в общем виде может быть представлена следующим образом:
Для каждой конкретной матрицы существует своя, одна-единственная система проверок. Проверки производятся по следующему правилу: в первую проверку вместе с проверочным разрядом входят информационные разряды, которые соответствуют единицам первого столбца проверочной матрицы П; во вторую проверку входит второй проверочный разряд В результате осуществления проверок образуется проверочный вектор, который называют синдромом. Если вес синдрома равен нулю, то принятая комбинация считается безошибочной. Если хотя бы один разряд проверочного вектора содержит единицу, то принятая комбинация содержит ошибку. Исправление ошибки производится по виду синдрома, так как каждому ошибочному разряду соответствует один-единственный проверочный вектор. Вид синдрома для каждой конкретной матрицы может быть определен при помощи проверочной матрицы Н, которая представляет собой транспонированную матрицу П, дополненную единичной матрицей, число столбцов которой равно числу проверочных разрядов кода:
Столбцы такой матрицы представляют собой значение синдрома для разряда, соответствующего номеру столбца матрицы Н. Процедура исправления ошибок в процессе декодирования групповых кодов сводится к следующему. Строится кодовая таблица. В первой строке таблицы располагаются все кодовые векторы. В первом столбце второй строки размещается вектор, вес которого равен 1. Остальные позиции второй строки заполняются векторами, полученными в результате суммирования по модулю 2 вектора Аналогично поступают до тех пор, пока не будут просуммированы с векторами все векторы По виду синдрома принятая комбинация может быть отнесена к тому или иному смежному классу, образованному сложением по модулю 2 кодовой комбинации с вектором ошибки Таблица6.1
Принятая кодовая комбинация Векторы
|

 (55)
(55)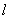 - число единиц в кодовом слове. Если бы не существовало условия постоянного веса, то число комбинаций кода могло бы быть гораздо большим, а именно. Примером кода с постоянным весом может служить стандартный телеграфный код № 3 (см. приложение 4). Комбинации этого кода построены таким образом, что на 7 тактов, в течение которых должна быть принята одна кодовая комбинация, всегда приходятся три токовые и четыре безтоковые посылки. Увеличение или уменьшение количества токовых посылок говорит о наличии ошибки.
- число единиц в кодовом слове. Если бы не существовало условия постоянного веса, то число комбинаций кода могло бы быть гораздо большим, а именно. Примером кода с постоянным весом может служить стандартный телеграфный код № 3 (см. приложение 4). Комбинации этого кода построены таким образом, что на 7 тактов, в течение которых должна быть принята одна кодовая комбинация, всегда приходятся три токовые и четыре безтоковые посылки. Увеличение или уменьшение количества токовых посылок говорит о наличии ошибки. (56)
(56) (57)
(57) (58)
(58)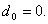
 (59)
(59) 60)
60) . (61)
. (61) (62)
(62)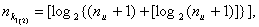 (63)
(63) (64)
(64) (65)
(65) (66)
(66) (67)
(67)
 (68)
(68) <="" div="" style="margin: 0px; padding: 0px; border: none; outline: 0px; font-size: 12px; vertical-align: baseline; background-color: transparent; background-position: initial initial; background-repeat: initial initial; ">
<="" div="" style="margin: 0px; padding: 0px; border: none; outline: 0px; font-size: 12px; vertical-align: baseline; background-color: transparent; background-position: initial initial; background-repeat: initial initial; "> (69)
(69) (70)
(70) будет приближаться к верхней границе в зависимости от того, насколько выражение под знаком логарифма приближается к целой степени двух.
будет приближаться к верхней границе в зависимости от того, насколько выражение под знаком логарифма приближается к целой степени двух.
 .
. , число столбцов равно +
, число столбцов равно +  (71)
(71) -коды, где, а соответствующие им матрицы называют порождающими, производящими, образующими.
-коды, где, а соответствующие им матрицы называют порождающими, производящими, образующими. (72)
(72)
 - вес соответствующей строки матрицы И. Если матрица И - единичная, то
- вес соответствующей строки матрицы И. Если матрица И - единичная, то  (удобство выбора в качестве матрицы И единичной матрицы очевидно: при
(удобство выбора в качестве матрицы И единичной матрицы очевидно: при  усложнилось бы как построение кодов, так и их техническая реализация).
усложнилось бы как построение кодов, так и их техническая реализация).
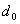 =2 производящая матрица С имеет вид
=2 производящая матрица С имеет вид
 порождающая матрица не может быть представлена в форме, общей для всех кодов с данным
порождающая матрица не может быть представлена в форме, общей для всех кодов с данным  соотношения п и. следующие: (3; 1), (7;4), (15; 11), (31; 26), (63; 57) и т. д.
соотношения п и. следующие: (3; 1), (7;4), (15; 11), (31; 26), (63; 57) и т. д. и, были исследованы Д. Слепяном в работе [10]. Для получения этих кодов матрица П должна иметь комбинации с максимальным весом. Для этого при построении кодов с последовательно используются векторы длиной п, весом
и, были исследованы Д. Слепяном в работе [10]. Для получения этих кодов матрица П должна иметь комбинации с максимальным весом. Для этого при построении кодов с последовательно используются векторы длиной п, весом  . Тем же Слепяном в работе [11] были исследованы неплотно упакованные коды с малой плотностью проверок на четность. Эти коды экономны с точки зрения простоты аппаратуры и содержат минимальное число единиц в корректирующих разрядах порождающей матрицы. При построении кодов с максимально простыми шифраторами и дешифраторами последовательно выбираются векторы весом = 2, 3,...,
. Тем же Слепяном в работе [11] были исследованы неплотно упакованные коды с малой плотностью проверок на четность. Эти коды экономны с точки зрения простоты аппаратуры и содержат минимальное число единиц в корректирующих разрядах порождающей матрицы. При построении кодов с максимально простыми шифраторами и дешифраторами последовательно выбираются векторы весом = 2, 3,..., 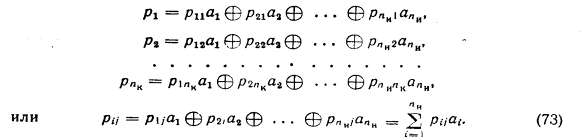

 и информационные разряды, соответствующие единицам второго столбца проверочной матрицы, и т. д. Число проверок равно числу проверочных разрядов корректирующего кода.
и информационные разряды, соответствующие единицам второго столбца проверочной матрицы, и т. д. Число проверок равно числу проверочных разрядов корректирующего кода.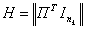 .
. c вектором, расположенным в соответствующем столбце первой строки. В первом столбце третьей строки записывается вектор
c вектором, расположенным в соответствующем столбце первой строки. В первом столбце третьей строки записывается вектор  , вес которого также равен 1, однако, если вектор
, вес которого также равен 1, однако, если вектор  , весом 1, с единицами в каждом из п разрядов. Затем суммируются по модулю 2 векторы, весом 2, с последовательным перекрытием всех возможных разрядов. Вес вектора определяет число исправляемых ошибок. Число векторов, определяется возможным числом неповторяющихся синдромов и равно (нулевая комбинация говорит об отсутствии ошибки). Условие неповторяемости синдрома позволяет по его виду определять один-единственный соответствующий ему вектор
, весом 1, с единицами в каждом из п разрядов. Затем суммируются по модулю 2 векторы, весом 2, с последовательным перекрытием всех возможных разрядов. Вес вектора определяет число исправляемых ошибок. Число векторов, определяется возможным числом неповторяющихся синдромов и равно (нулевая комбинация говорит об отсутствии ошибки). Условие неповторяемости синдрома позволяет по его виду определять один-единственный соответствующий ему вектор 
 сравнивается с векторами, записанными в строке, соответствующей полученному в результате проверок синдрому. Истинный код будет расположен в первой строке той же колонки таблицы. Процесс исправления ошибки заключается в замене на обратное значение разрядов, соответствующих единицам в векторе ошибок.
сравнивается с векторами, записанными в строке, соответствующей полученному в результате проверок синдрому. Истинный код будет расположен в первой строке той же колонки таблицы. Процесс исправления ошибки заключается в замене на обратное значение разрядов, соответствующих единицам в векторе ошибок. не должны быть равны ни одномуиз векторов, в противном случае в таблице появились бы нулевые векторы.
не должны быть равны ни одномуиз векторов, в противном случае в таблице появились бы нулевые векторы.


