Тема 2. Условная энтропия и энтропия объединения
Понятие условной энтропии в теории информации используется при определении взаимозависимости[3] между символами кодируемого алфавита, для определения потерь при передаче информации по каналам связи, при вычислении энтропии объединения. Во всех случаях при вычислении условной энтропии в том или ином виде используются условные вероятности. Если при передаче n сообщений символ А появился m раз, символ В появился l раз, а символ А вместе с символом В – к раз, то вероятность появления символа А
Если известна условная вероятность, то можно легко определить и вероятность совместного появления символов А и В, используя выражения (7)
От классического выражения (4) формула условной энтропии отличается тем, что в ней вероятности – условные:
где индекс i выбран для характеристики произвольного состояния источника сообщения А, индекс j выбран для характеристики произвольного состояния адресата В. Различают понятия частной и общей условной энтропии. Выражение (9) и (10) представляют собой частные условные энтропии. Общая условная энтропия сообщения В относительно сообщения А характеризует количество информации, содержащейся в любом символе алфавита, и определяется усреднением по всем символам, т. е. по всем состояниям с учетом вероятности появления каждого из состояний, и равна сумме вероятностей появления символов алфавита на неопределенность, которая остается после того, как адресат принял сигнал
Выражение (11) является общим выражением для определения количества информации на один символ сообщения для случая неравномерных и взаимонезависимых символов. Так как
Понятие общей и частной условной энтропии широко используется при вычислении информационных потерь в каналах связи с шумами. В общем случае, если мы передаем m сигналов А и ожидаем получить m сигналов В, влияние помех в канале связи полностью описывается канальной матрицей, которую мы приводим ниже:
Вероятности, которые расположены по диагонали, определяют правильный прем, остальные – ложный. Значение цифр, заполняющих колонки канальной матрицы, обычно уменьшаются по мере удаления от главной диагонали и при полном отсутствии помех всех, кроме цифр, расположенных на главной диагонали, равны нулю. Если описывать канал связи со стороны источника сообщений, то прохождение данного вида сигнала в данном канале связи описывается распределением условных вероятностей вида, так для сигнала распределением вида (13) (14) (15) (16)
(17) (18)
(19)
|

 ; вероятность появления символа В; вероятность совместного появления символов А и В
; вероятность появления символа В; вероятность совместного появления символов А и В  ; условная вероятность появления символа А относительно символа В и условная вероятность появления символа В относительно символа А
; условная вероятность появления символа А относительно символа В и условная вероятность появления символа В относительно символа А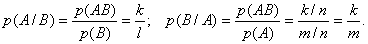 (7)
(7) (8)
(8) (9)
(9) (10)
(10) (11)
(11) представляет собой вероятность совместного появления двух событий
представляет собой вероятность совместного появления двух событий  , то формула (11) можно записать следующим образом:
, то формула (11) можно записать следующим образом: (12)
(12)


 …………………………………………………………..
………………………………………………………….. 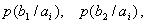
 ……………………………………………………………
……………………………………………………………



