Взаимосвязь румбов и дирекционных углов

№ четверти	Пределы четверти	Название румба	Зависимость
I	0°-90°	CВ	r = a
II	90°-180°	ЮВ	r = 180°- a
III	180°-270°	ЮЗ	r = a - 180°
IV	270°-360°	СЗ	r = 360°- a

 

Вычисленные значения румбов записывают в графу 6 (табл.4).

Горизонтальные проложения сторон теодолитного хода d определяют по измеренным на местности длинам сторон D_ср и углам наклона сторон к горизонту g по формуле:

d = D_ср×cos g.

Если углы наклона g < 1°30, то горизонтальные проложения равны измеренным длинам сторон теодолитного хода.

В примере только сторона хода 3-4 имеет угол наклона более 1˚30, поэтому:

a_3-4 = 158,32

Вычисленные значения горизонтальных проложений d записывают в графу 7 (табл.4), после чего определяют периметр теодолитного хода:

Р = d_1-2 + d_2-3 + …….. + d_{n – n+1}.

 

2.2.6. Вычисление и увязка приращений координат сторон теодолитного хода

 

Приращения прямоугольных координат находят по формулам:

±DX_i = d_i × cos r_i;

±DU = d_i × sin r_i.

Знаки приращений координат определяют по названию румба:

СВ (+Х,+Y);		ЮВ (-Х, Y);
ЮЗ(-Х,-Y);		СЗ (+Х, -Y).

Вычисленные приращения координат с соответствующим знаком записывают в графу 8 и 10 (табл.4).

Вычисляют алгебраическую сумму приращений координат по оси Х åDX_выч и оси Y åDU_выч и записывают в нижней части графы 8 и 10 (табл. 4).

Затем определяют линейные невязки приращений координат f_x по оси Х и f_y по оси Y:

Поскольку теодолитный ход замкнутый, то

Полученные невязки записывают в нижней части графы 8 и 10 (табл.4).

Вычисляют абсолютную невязку f_АБС в замкнутом теодолитном ходе по формуле:

f_АБС = Ö f²_x + f²_y.

Для оценки точности линейных измерений в теодолитном ходе вычисляют относительную невязку:

,

где p– периметр замкнутого теодолитного хода.

Относительную невязку f_ОТНсчитают допустимой, если она не превышает предельную относительную невязку, которую принимают 1:2000.

Если f_ОТН окажется допустимой, то невязки f_Х и f_Y распределяютс обратным знаком на соответствующие приращения координат пропорционально горизонтальным проложениям сторон теодолитного хода:

Контролем служит равенство суммы поправок по осям (Х, Y) линейной невязке по этим осям, т. е.

Полученные поправки округляют до сотых долей метра и записывают в графы 9 и 11.

Вычисляют исправленные приращения координат:

 

 

которые записывают в графы 12 и 13 (табл.4).

Вычисляют алгебраическую сумму приращений координат по осям (X, Y) они должны быть равны 0, т.е.:
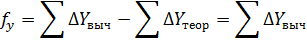