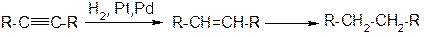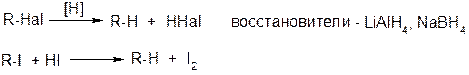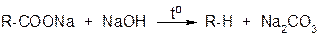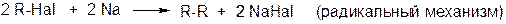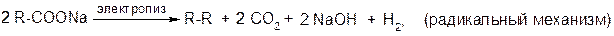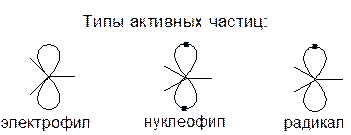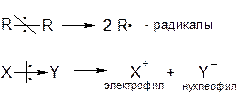Способы получения алканов. Важной нелинейной операцией над векторами является скалярное произведение векторов.
Алканы
Углеводороды общей формулы – CnH2n+2. Гомологический ряд алканов.
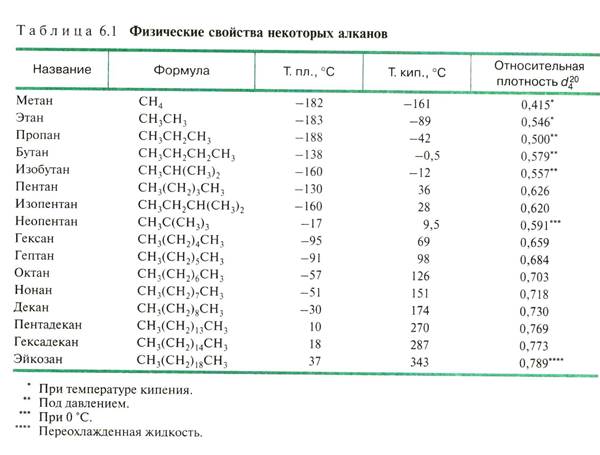
Физические свойства алканов – см. учебник.
Способы получения алканов
Источники промышленного получения алканов – природный газ, нефть.
Синтетические способы (применяются, в основном, в лабораторных условиях для получения сложных алканов):
1. Гидрирование алкенов и алкинов
2. Восстановление галогеналканов
3. Реакция Дюма
4. Реакция Вюрца
5. Реакция Кольбе
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ (вставка)
Химическая реакция – это, как правило, многостадийный процесс. Она начинается с разрыва связей в исходных соединениях, после чего образуются новые связи и новые соединения. В ходе реакции образуются неустойчивые промежуточные частицы. Последовательность всех стадий называется механизмом реакции. Активные частицы – это частицы, обладающие высокой химической активностью, они инициируют реакцию.
Электрофил – электронодефицитная частица, атакует в места повышенной электронной плотности. Нуклеофил – электроноизбыточная частица, атакует в места пониженной электронной плотности. Радикал – электронейтральная частица, атакует неполярные и малополярные связи.
Активные частицы могут образоваться в результате разрыва химической связи. Малополярные связи разрываются гомолитически, и образуются два радикала; полярные связи разрываются гетеролитически, и образуются нуклеофил и электрофил:
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
|