Методы прогнозной экстраполяции
Одним из наиболее распространенных методов статистического прогнозирования является экстраполяция, т.е. распространение прошлых и настоящих закономерностей, связей и соотношений на будущее. Цель такого прогноза показать к каким результатам можно прийти в будущем, если к нему двигаться с той же скоростью или ускорением, что и в прошлом. Экстраполяционный прогноз определяет варианты экономического развития, исходя из гипотезы, что основные факторы и тенденции прошлого периода сохраняются на период прогноза, или, что можно обосновать и учесть направления их изменений в рассматриваемый период. Подобная гипотеза выдвигается, исходя из инерционности социально-экономических явлений и процессов. Инерционность развития экономики связана с длительно воздействующими факторами, например, такими, как структура основных фондов, их возраст и эффективность, степень устойчивости технологических взаимосвязей отрасли производства и др. Для достаточно точного количественного измерения ожидаемых значений признака необходимо, чтобы прогностическая модель имела достаточную точность или допустимо малую ошибку прогноза. Ошибка статистического прогноза будет тем меньше, чем меньше срок упреждения и чем длиннее база прогноза. В большинстве случаев срок упреждения не должен превышать третьей части длины базы прогноза. В каждом конкретном исследовании значения длин базы прогноза и срока упреждения необходимо обосновать, используя имеющуюся информацию об особенностях изучаемого объекта. Методы прогнозной экстраполяции подразделяются на простые и сложные. Простые исходят из предположения относительно постоянства в будущем абсолютных значений уровней среднего уровня ряда, среднего абсолютного прироста, среднего темпа роста. а) экстраполяция на основе средней В самом простом случае, на предположении о том, что средний уровень ряда не имеет тенденцию к изменению или если это изменение незначительно, можно принять
где yi+1 - прогнозируемое значение,
yi – фактическое значение показателя в i - период
Подобная экстраполяция дает точечную оценку. Однако, поскольку подобные прогнозы основываются на информации о поведении объекта в прошлом, то они всегда будут иметь ошибку. Следовательно, каждый прогноз характеризуется двумя основными показателями: а) значением прогнозного показателями на будущий момент времени, выработанным каким либо методом прогнозирования, т.е. сам прогноз б) стандартной ошибкой (отклонением) прогноза, который характеризует разброс прогнозируемого значения вокруг реального. δ =
б) экстраполяция по среднему темпу роста: yi+1 = k *yn, где yi+1 – прогнозируемая величина; k – средний темп роста; yn – последнее значение фактора в ряду. При этом средний темп роста определяется по следующей формуле k = где n – число периодов, y1 – первое значение фактора в ряду.
в) экстраполяция по среднему абсолютному приросту yi+1 = yn + Δ y , где yi+1 – прогнозируемая величина; yn – последнее значение фактора в ряду; Δ y – средний абсолютный прирост. При этом средний абсолютный прирост определяется по формуле: Δ y = где yn – последнее значение фактора в ряду; y1 – первое значение фактора в ряду; n – число периодов.
Сложные методы экстраполяции основаны на выявлении тренда. Под трендом понимается характеристика основной закономерности движения во времени, в некоторой мере свободной от случайных воздействий. Тренд – это длительная тенденция изменения экономических показателей. Экстраполяция тренда может быть применена только в том случае, если развитие явления достаточно хорошо описывается построенной моделью и условия, определяющие тенденцию развития в прошлом, не претерпят изменений в будущем. К методам сложной экстраполяции относят следующие методы: ¨ аналитического выравнивания динамических рядов; ¨ экспоненциального сглаживания; ¨ скользящих средних. Аналитическое выравнивание – это нахождение математической функции, которая наиболее точно описывает тенденцию изменений исследуемого явления. Наиболее ответственными этапами аналитического выравнивания являются: - выбор кривой, отражающей тенденцию; - определение показателей, дающих количественную характеристику тенденции изменения; - оценка достоверности прогнозных расчетов. Выбор кривой можно осуществить на основе построения графика. Общий вид графика, как правило, позволяет установить имеет ли динамический ряд показателя отчетливо выраженную тенденцию, если да, то является ли эта тенденция плавной, каков характер тенденции (возрастающая, убывающая). Отвечая на эти вопросы, необходимо помнить, что внешняя простота графика обманчива. Любая динамическая задача гораздо сложнее статистической, и каждая точка кривой есть результат изменения явления и в пространстве и во времени. Динамика изменения показателя бывает достаточно сложной, поэтому ее не всегда удается выразить элементарными аналитическими функциями (прямая, парабола …). Как правило, для повышения обоснованности и достоверности выравнивания с целью более точного выявления имеющейся тенденции желательно проводить вариантный расчет по нескольким функциям, и на основе экспертных и статистических оценок определять лучшую форму связи. После определения формы связи и выбора подходящих математических кривых задача сводится к определению показателей, которые дадут количественную характеристику. Необходимо определить параметры уравнений связи. Для их нахождения лучше всего пользоваться методом наименьших квадратов. Выравнивающая функция в этом случае будет занимать такое положение среди фактических значений показателя, при котором сумма квадратов отклонений точек от функции будет минимальной.
где
N – число наблюдений. Оценка достоверности прогнозных расчетов проводится с использованием приемов математической статистики, а также графиков. Метод скользящих средних.. Часто ряды динамики характеризуются резкими колебаниями показателей по годам. Такие ряды, как правило, имеют слабую связь со временем и не обнаруживают тенденции к росту или снижению. В такой ситуации можно использовать метод скользящих средних. Метод скользящих средних позволяет отвлечься от случайных колебаний временного ряда, что достигается путем замены значений внутри выбранного интервала средней арифметической величиной. Интервал, величина которого остается постоянной, постоянно сдвигается на одно наблюдение. Величина интервала (Р) может принимать любое значение от минимального (Р=2) до максимального (Р= n-1), где n – длина рассматриваемого временного ряда. Сглаженный ряд короче первоначального на (Р-1) наблюдение. При использовании метода скользящих средних прежде всего определяется величина интервала сглаживания (Р), обеспечивающая взаимное погашение случайных отклонений во временном ряду. Выбор величины интервала должен осуществляться с учетом особенностей ряда. Если наблюдается определенная цикличность изменения показателей, интервал скольжения должен быть равен продолжительности цикла. При отсутствии цикличности в изменении показателей рекомендуется производить многовариантный расчет при меняющемся параметре скольжения. Метод экспоненциального сглаживания. Между достигнутым в текущем году уровнем показателя и уровнями его в прошлые годы существует определенная связь. С увеличением периода времени связь уровней ослабевает, а значит, результаты более поздних наблюдений несут большую информацию об ожидаемом уровне показателя. Поэтому, при прогнозировании большее значение следует придавать последним показателям динамических рядов. Этому принципу отвечает метод экспоненциального сглаживания, разработанный Р.Брауном. Экспоненциальное сглаживание- это вид выравнивания особенно сильно колеблющихся динамических рядов в целях последующего прогнозирования. Данный метод позволяет давать обоснованные прогнозы на основании рядов динамики, имеющих умеренную связь со временем, и обеспечивает больший учет показателей, достигнутых в последние годы. Сущность метода экспоненциального сглаживания заключается в сглаживании временного ряда с помощью взвешенной скользящей средней. При проведении исследований целесообразно применять метод для линейной и параболической тенденций. При линейной функции тренд выражается двумя членами ряда Тейлора и некоторым малым числом Еt, зависящем от времени. При параболической функции тренд выражается тремя членами ряда Тейлора и некоторым малым числом Еt, зависящем от времени. Основными показателями экспоненциального сглаживания являются: характеристики сглаживания, оценки коэффициентов, начальные условия. При выборе начальных условий коэффициенты рассчитывают путем выравнивания исходного временного ряда способом наименьших квадратов, предполагая соответственно линейную (параболическую) тенденцию изменений. Процесс экспоненциального сглаживания основывается на цепочечных расчетах. Сначала определяются исходные параметры выравнивающих кривых, по которым с помощью формул находят начальные условия. На основе начальных условий по формулам определяют характеристики сглаживания, затем – оценки коэффициентов для экспоненциального сглаживания первого значения в исходном динамическом ряду. И на конец – расчетное значение соответствующей функции. Полученные на этом первом этапе характеристики сглаживания затем используются в качестве исходных данных для вычисления второго сглаженного значения в рассматриваемом динамическом ряду и т.д. Вычисления продолжают до тех пор, пока не будут сглажены все значения исходного временного ряда. Результаты прогноза в значительной мере зависят от параметра сглаживания (
Прогнозирование на основе регрессионных моделей. Регрессионные модели для прогнозирования используются в тех случаях, когда может быть определено существенное влияние одного или нескольких факторов на динамику прогнозируемой переменной. Для прогнозных расчетов на основе регрессионных моделей необходимо иметь плановые или прогнозные значения выбранных факторов на перспективу, которые необходимо подставить в уравнения. Достоинство регрессионных моделей состоит в том, что наличие зависимости одного явления от других лучше поддается содержательной интерпретации, чем простая экстраполяция трендов. Кроме того, регрессионные модели создадут базу для расчетного экспериментирования с целью получения ответов на вопросы типа «что будет, если …». Производственные функции (функции производственных затрат) – это регрессионные модели, используемые в анализе и прогнозировании экономических объектов, характеризующие обобщенные зависимости между затратами ресурсов и выпуском продукции.
5. Методы моделирования (самостоятельно)
|

 yi+1 = y =
yi+1 = y =  / n,
/ n, y – среднее значение ряда,
y – среднее значение ряда,
 ,
, ,
,
 min
min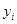 – фактическое значение показателей,
– фактическое значение показателей,
 - вычисленное по выравнивающему уравнению,
- вычисленное по выравнивающему уравнению, ). В случае его малых величин при прогнозировании учитываются все прошлые наблюдения, в случае больших значений – в основном последние. Существуют различные подходы к выбору параметра сглаживания. Наиболее простым, является определение параметра сглаживания, как величины, очень близкой к обратному значению параметра сглаживания Р при расчете скользящих средних.
). В случае его малых величин при прогнозировании учитываются все прошлые наблюдения, в случае больших значений – в основном последние. Существуют различные подходы к выбору параметра сглаживания. Наиболее простым, является определение параметра сглаживания, как величины, очень близкой к обратному значению параметра сглаживания Р при расчете скользящих средних.


