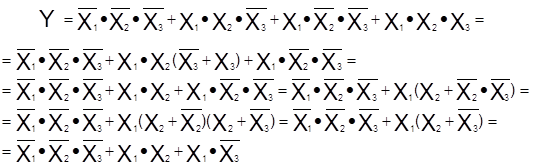Основные теоретические положения
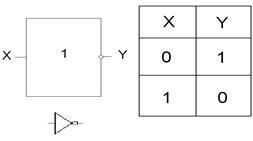
Математической основой цифровой электроники и вычислительной техники является алгебра логики или булева алгебра (по имени английского математика Джона Буля). В булевой алгебре независимые переменные или аргументы (X) принимают только два значения: 0 или 1. Зависимые переменные или функции (Y) также могут принимать только одно из двух значений: 0 или 1. Булева функция представляется в виде: Y = F (X1; X2; X3... XN). Данная форма задания булевой функции называется алгебраической. Основными логическими функциями являются (таблицы истинности представлены на рис. 1…9): – логическое отрицание (инверсия) Y= – логическое сложение (дизьюнкция) Y=X1+X2 или Y=X1VX2; – логическое умножение (коньюнкция) Y=X1·X2 или Y=X1LX2. – функция равнозначности (эквивалентности) Y=X1·X2+ – функция неравнозначности (сложение по модулю два) – функция Пирса (логическое сложение с отрицанием) – функция Шеффера (логическое умножение с отрицанием) Y= Для булевой алгебры справедливы следующие законы и правила: – распределительный закон X1·(X2+X3)=X1·X2+X1·X3; X1+X2·X3=(X1+X2)·(X1+X3); – правило повторения X·X=X; X+X=X; – правило отрицания X· – теорема де Моргана – тождества X·1=X; X+0=X; X·0=0; X+1=1. – правило поглощения Схемы, реализующие логические функции, называются логическими элементами. Основные логические элементы имеют, как правило, один выход (Y) и несколько входов, число которых равно числу аргументов (X1;X2;X3... XN). На электрических схемах логические элементы обозначаются в виде прямоугольников с выводами для входных (слева) и выходных (справа) переменных. Внутри прямоугольника изображается символ, указывающий функциональное назначение элемента. На рис.1…9 представлены два вида условных обозначений логических элементов, реализующих рассмотренные в п.2.2. функции. Там же представлены так называемые таблицы состояний (таблицы истинности), описывающие соответствующие логические функции в двоичном коде в виде состояний входных и выходных переменных. Таблица истинности является также табличным способом задания логической функции. На рис.1 представлен элемент “НЕ”, реализующий функцию логического отрицания Y =
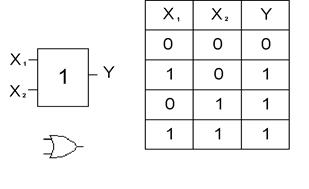
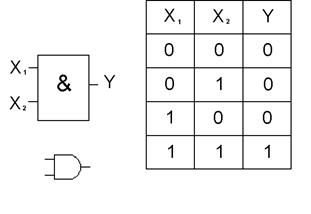
Рис. 1 Элемент “ИЛИ” (рис.2) и элемент “И” (рис.3) реализуют функции логического сложения и логического умножения соответственно.
Рис. 2
Рис. 3
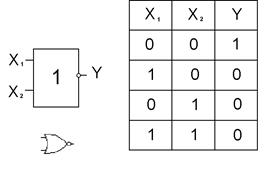
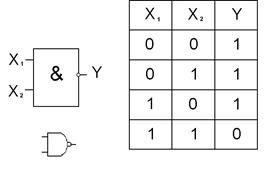
Функции Пирса и функции Шеффера реализуются с помощью элементов “ИЛИ-НЕ” и “И-НЕ”, представленных на рис.4 и рис. 5 соответственно.
Рис. 4
Рис. 5
Элемент Пирса можно представить в виде последовательного соединения элемента “ИЛИ” и элемента “НЕ” (рис.6), а элемент Шеффера - в виде последовательного соединения элемента “И” и элемента “НЕ” (рис.7).
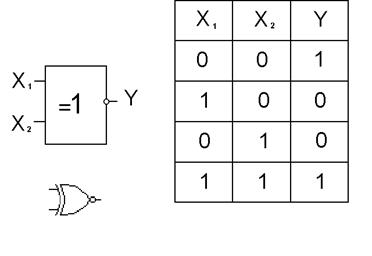
На рис.8 и рис.9 представлены элементы “Исключающее ИЛИ” и “Исключающее ИЛИ - НЕ”, реализующие функции неравнозначности и неравнозначности с отрицанием соответственно.
Рис. 8
Рис. 9
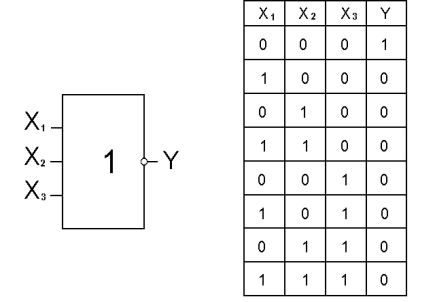
Логические элементы, реализующие операции конъюнкции, дизъюнкции, функции Пирса и Шеффера, могут быть, в общем случае, n - входовые. Так, например, логический элемент с тремя входами, реализующий функцию Пирса, имеет вид, представленный на рис.10.
Рис.10
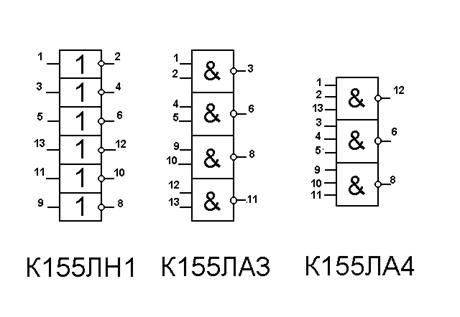
В таблице истинности (рис.10) в отличие от таблиц в п.2.4. имеется восемь значений выходной переменной Y. Это количество определяется числом возможных комбинаций входных переменных N, которое, в общем случае, равно: N = 2 n, где n - число входных переменных. Логические элементы используются для построения интегральных микросхем, выполняющих различные логические и арифметические операции и имеющих различное функциональное назначение. Микросхемы типа К155ЛН1 и К155ЛА3, например, имеют в своем составе шесть инверторов и четыре элемента 2И-НЕ соответственно, микросхема К155ЛА4 содержит три элемента 3И-НЕ (рис.11), а микросхема К155ЛР1 содержит два элемента 2И-2ИЛИ-НЕ, один из которых показан на рис. 12.
Рис. 11
Рис. 12 Цифрами на рис. 11 отмечены номера соответствующих выводов микросхем, отсчитываемые против часовой стрелки от первого вывода, помеченного точкой на корпусе микросхемы. Общий вывод (7) и вывод (14) для питания микросхемы (+5 В) на рисунке не показаны. Логическую функцию любой сложности можно реализовать с помощью указанных логических элементов. В качестве примера рассмотрим функцию, заданную в алгебраической форме, в виде:
Упростим данную функцию, используя вышеприведенные правила:
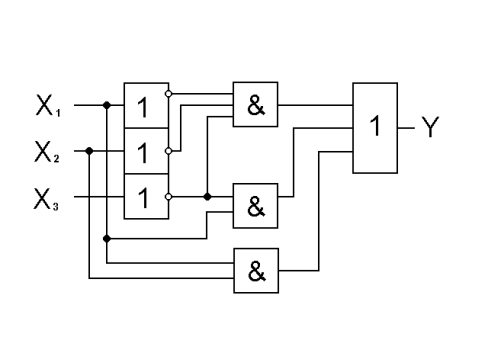
Проведенная операция носит название минимизации логических функций и служит для упрощения функциональной схемы соответствующего цифрового устройства. Функциональная схема устройства, реализующая рассматриваемую функцию, представлена на рис.13.
Рис. 13
Следует отметить, что полученная после преобразований функция (2) не является полностью минимизированной. Полная минимизация функции проводится в процессе выполнения лабораторной работы.
|

 ;
;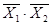 или Y=X1~X2;
или Y=X1~X2;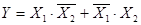 или Y=X1
или Y=X1  X2;
X2;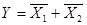 ;
; =0, X+
=0, X+ 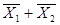 =
= 


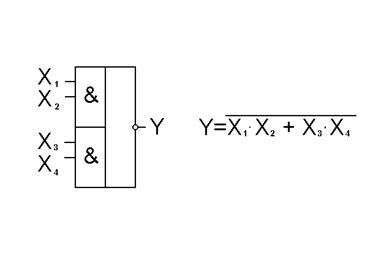
 . (1)
. (1)