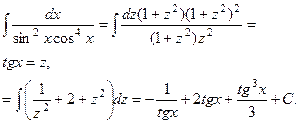Интегрирование рациональных дробей.При интегрировании рациональных дробей следует придерживаться такого порядка. 1. Проверить, будет ли данная дробь правильной, если дробь неправильная, то выделить целую часть. 2. Проверить, будет ли дробь простейшей, если будет, то проинтегрировать ее. 3. Разложить знаменатель на простейшие действительные множители. Q(x) = a0 (x – a) (x - b)…(x – c)k …(x2 + px +q)….(x2 + p1 x +q1)l….., где x2 + px + q – квадратный трехчлен, не разлагающийся на действительные множители. 4. Представить дробь как сумму простейших дробей. При этом
5. Найти коэффициенты и проинтегрировать.
П р и м е р ы.
5x2 + 9x + 4
Интегралы от рациональных функций всегда и при том стандартным образом выражаются через элементарные функции. Метод рационализации – это такой метод, когда с помощью подстановки данный интеграл приводится к интегралу от рациональной функции. 1. Сделаем замену: ax + b = ts, s = OHЗ дробей m/n, p/q, …. Интеграл сводится к интегралу от рациональной функции, т.к. П р и м е р.
2. Универсальная тригонометрическая подстановка.
Если в данный интеграл подставить выражения для sinx, cosx и dx, то получим интеграл от рациональной функции.
Универсальная тригонометрическая подстановка приводит в ряде случаев к сложным рациональным дробям. 3.
x П р и м е р.
|
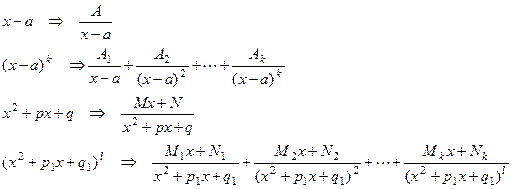
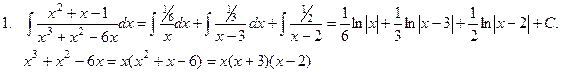
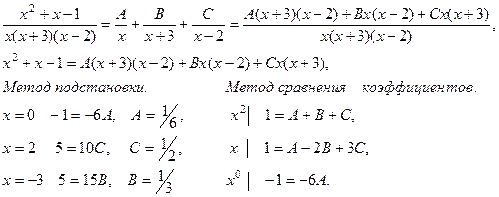
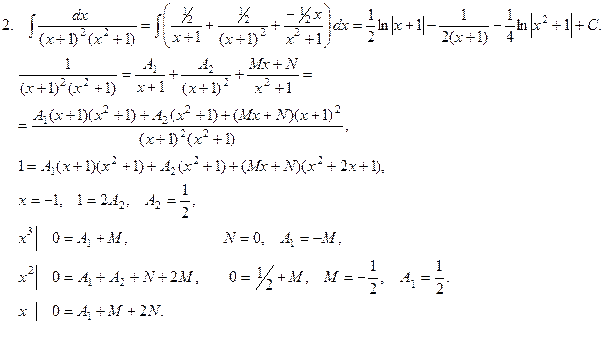
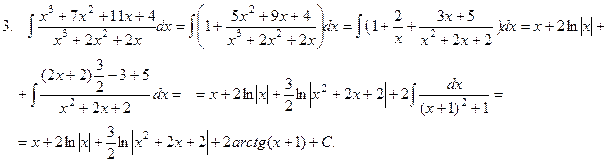
x3 + 7x2 + 11x + 4 x3 + 2x2 + 2x
x3 + 2x2 + 2x 1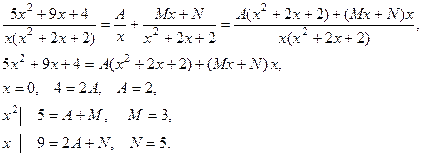
Методы рационализации.
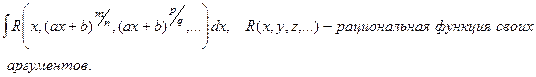
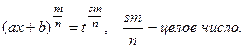
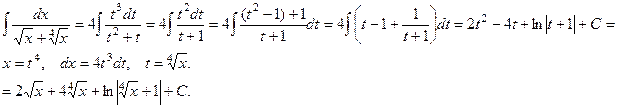
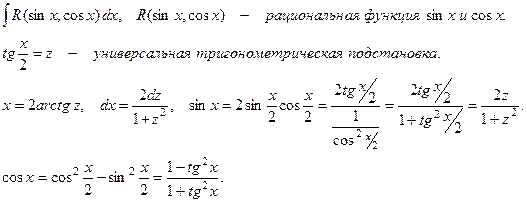
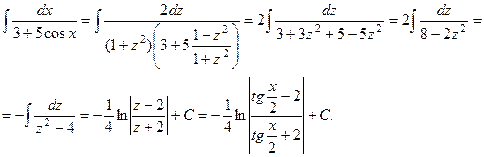
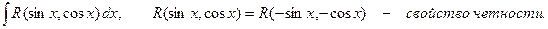
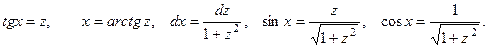
z
