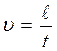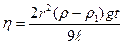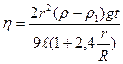Краткие теоретические сведения. Жидкость также как и газ обладает свойством перемещаться из области большого давления в область меньшего давления
Жидкость также как и газ обладает свойством перемещаться из области большого давления в область меньшего давления. Такое перемещение называется течением жидкости. Различают два вида течения жидкости: лиминарное (слоистое) и тербулентное (вихревое). Ламинирным течением называют течение, при котором слои жидкости скользят друг по другу. Оно происходит при небольших скоростях движения в трубках с относительно гладкими стенками, без резких изменения площади сечения или направления, а также при отсутствии множественных разветвлений. Турбулентным называется такое течение, при котором слои жидкости перемешиваются. Оно возникает при резких сужениях сечения трубки, при значительной шероховатости поверхности стенок трубы, а также в местах множественного разветвления русла или трубы, по которой течет жидкость. Течение жидкости при небольших скоростях носит ламинарный характер вследствие сил взаимного притяжения между молекулами жидкости, а также между молекулами жидкости и твердых тел, с которыми жидкость соприкасается в процессе течения.
Рис.1 Ламинарное течение жидкости можно изобразить в виде параллельно перемещающихся слоев, распределены так, как это показано на рисунке 1, где стрелки представляют векторы скорости движения жидкости. Наибольшая скорость наблюдаются в средней, прилегающей к оси части трубы; по мере приближения к стенкам скорость уменьшается, а слой, непосредственно, прилегающий к стенкам трубы, покоится. Таким образом, вся масса текущей жидкости разделена по слоям, движущихся с различными скоростями, между которыми действуют силы внутреннего трения, препятствующие перемещению одного слоя относительно другого. Величина силы внутреннего трения зависит от градиента скорости и площади соприкосновения слоев и выражается Формулой:
где F – сила внутреннего трения.
ΔS – площадь сопротивления слоев. Формула (1) представляет собой закон Ньютона для вязкости: сила внутреннего трения пропорциональна градиенту скорости, площади соприкосновения слоев и направлена против движения жидкости. Коэффициент внутреннего трения является важной характеристикой жидкости. В зоотехнии и ветеринарии изучают вязкость молока, крови, меда, и т. п. как показатель состояния здоровья животного, качества продукции. Из формулы (1) следует физический смысл коэффициента внутреннего трения: коэффициент внутреннего трения численно равен силе внутреннего трения, действующей между слоями единичной площади при градиенте скорости, равному единице. Коэффициент внутреннего трения зависит от природы жидкости и ее температуры. С повышением температуры коэффициент внутреннего трения уменьшается, т. к. увеличивается среднее расстояние между молекулами, а значит, уменьшаются силы взаимного притяжения между ними. В системе СИ коэффициент вязкости измеряется в Н*с/м2 = Па*с = кг/м*с, а в системе СГС в г/см*с. Последняя система единиц называется пуаз. Изучая ламинарное течение жидкости, французский физик и физиолог Пуазейль в 1841 г установил закон, согласно которому средняя скорость ламинарного течения жидкости по трубе пропорциональна градиенту давления жидкости, квадрату радиуса трубы и обратно пропорциональна коэффициенту внутреннего трения жидкости:
где
r- радиус трубы; ή-коэффициент внутреннего трения. Знак минус в формуле (2) показывает, что скорость течения жидкости направлена противоположно градиенту давления. Из закона Паузелия (2) можно получить формулу для определения объема жидкости, протекшей по трубе за некоторый промежуток времени t: V=
где r-радиус трубы;
t-время течения жидкости по трубе; ή-коэффициент внутреннего трения;
V-объем жидкости, протекшей по трубе завремя. Формула (3) лежит в основе метода определения коэффициента внутреннего трения с помощью капиллярного вискозиметра.
ЗАДАНИЕ I: определение коэффициента внутреннего трения жидкости капиллярным вискозиметром. ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: капиллярный вискозиметр, исследуемая жидкость дистиллированная вода, термометр, резиновая груша.
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙУСТАНОВКИ.
Рис.2 Капиллярный вискозиметр представляет собой U-образную стеклянную трубку рис.2, широкое колено, которой имеет внизу шарообразное расширение А. Капиллярная часть вискозиметра К имеет в своей верхней части шарик Б, переходящий затем в широкую трубку В. Шарик Б имеет метки М и Н, которые ограничивают определенный объем исследуемой жидкости. С помощью пипетки через широкое колено заполняют вискозиметр исследуемой жидкостью так, чтобы заполнился шарик А. С помощью груши через трубку В всасывают воздух так, чтобы уровень жидкости в вискозиметре Так как жидкость течет по капилляру под действием собственного веса, то разность давлений на концах капилляра будет равна гидростатическому давлению:
где ρ -плотность жидкости, g -ускорение силы тяжести, h -высота столба жидкости. Учитывая это, формулу (3) можно записать в виде:
Из формулы (4) видно, что для определения коэффициента внутреннего трения η надо знать время течения жидкости по капилляру, радиус и длину капилляра, плотность жидкости, высоту поднятия ее в капилляре, а также объем протекшей жидкости. Чтобы не делать таких затруднительных измерений, применяют метод сравнения. Для этого вначале проделывают опыт с дистиллированной водой, а затем с исследуемой жидкостью. Запишем формулу (4) для дистиллированной воды и исследуемой жидкости: -для воды:
-для исследуемой жидкости:
где
t0 --время протекания через капилляр воды, tx -время протекания через капилляр жидкости. В формулах (5) и (6) левые части равны, следовательно, равны и правые части:
Тогда получим:
Формула (7) является расчетной для определения коэффициента внутреннего трения капиллярным вискозиметром. Для поддержания постоянной температуры исследуемой жидкости во время эксперимента вискозиметр опускают в сосуд с водой С.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.
1.Чистый вискозиметр ополосните дистиллированной водой, а затем налейте в него дистиллированную воду так, чтобы заполнился нижний шарик А. Погрузите вискозиметр в сосуд с водой. 2.Осторожно с помощью резиновой груши засосите воду в верхний шарик Б чуть выше метки М. 3.Уберите резиновую грушу и секундомером определите время t0, в течении которого мениск воды пройдет расстояние от метки М до метки Н. 4.опыт проделайте 3-5 раз и вычислите среднее значение времени течения воды tоср. 5.Вылейте воду из вискозиметра и ополосните его исследуемой жидкостью. 6.Залейте в вискозиметр исследуемую жидкость до того же уровня, что и воду. 7.Так же, как и для дистиллированной воды, определите время tx течения жидкости от метки М до метки Н. 8.Опыт повторите 3-5 раз и вычислите среднее значение времени течения жидкости t x ср. 9.Измерьте температуру воды в сосуде С. 10.Выпишете из таблиц значения плотности воды ρ0, плотности исследуемой жидкости ρx и коэффициента внутреннего трения воды 11.Вычислите коэффициент внутреннего трения жидкости по формуле (7), подставляя средние значения txср и t0ср. 12.Расчитайте абсолютные ошибки измерений времени 13.Вычислите относительную ошибку измерений коэффициента внутреннего трения жидкости по формуле:
14.Вычислите абсолютную ошибку коэффициента внутреннего трения по формуле:
15.Данные измерений занесите в таблицу 1 и 2:
Таблица 1. Постоянные величины
Таблица 2 Результаты измерений
16.Сделайте выводы.
ЗАДАНИЕ 2: Определение коэффициента внутреннего трения жидкости методом падающего шарика (метод Стокса). ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: цилиндр с исследуемой жидкостью, набор шариков, секундомер, термометр.
ОПИСАНИЕ ЭКСПРИМЕНТАЛЬОЙ УСТАНОВКИ. Всякая реальная жидкость обладает вязкостью и поэтому тело, движущееся в жидкости, испытывает на себе силы сопротивления со стороны жидкости. Подчеркнем, что здесь играет роль не трение шарика о жидкость, а трение отдельных слоев жидкости друг о друга, так как при соприкосновении твердого тела с жидкостью, к поверхности тела тотчас же прилипают молекулы жидкости, образуя молекулярный слой жидкости, обволакивающий тело. Слой жидкости, непосредственно прилегающий к телу, будет двигаться со скоростью тела и увлекать за собой соседние слои жидкости, которые тоже начнут двигаться. Таким образом, при небольших скоростях движения тела в жидкости будет происходить ламинарное течение жидкости в направлении траектории движения тела. Английский физик Стокс установил закон: для тела шарообразной формы, движущегося с небольшой скоростью в жидкости, сила сопротивления F пропорциональна коэффициенту внутреннего трения η, радиусу шара r и скорости движения шара ν:
В данной работе для определения коэффициента внутреннего трения жидкости используется стеклянный цилиндр с исследуемой жидкостью(рис.3).На стекле цилиндра нанесены две метки: метка начала отсчета времени падения шарика(1) и окончания(2). Рассмотрим падение шарика вязкой покоящейся жидкости. На шарик действуют три силы: сила тяжести
сила сопротивления (сила Стокса)
Выталкивающая сила (по закону Архимеда равна весу вытесненной шариком жидкости). F1 = 4/3πr2 ρ0g где ρ0 – плотность вещества, r – его радиус. g – ускорение силы тяжести, η – коэффициент внутреннего трения жидкости, υ – скорость падения шарика, ρ1 – плотность жидкости, Направления этих сил указаны на рисунке 3.
В процессе движения шарика силы ρ и F1 не изменятся, а сила сопротивления F будет увеличиваться по мере увеличения скорости движения шарика (вначале шарик движется ускоренно. Наступит такой момент, когда силы F1 и F уравновесят силу тяжести, и тогда шарик будет двигаться равномерно. Следовательно, при условии: Р = F1+F шарик падает с постоянной скоростью, которую можно определить, зная пройденный путь и время:
Учитывая (9, 10, 11), и равенство (12) можно записать в виде: 4/3 πr3ρg = 4/3 πr3ρ1g + 6πrηυ. Отсюда после преобразования (учитывая формулу (13)) получим:
Заметим, что все наши рассуждения верны лишь в том случае, если шарик падает в безгранично простирающейся жидкости, что практически осуществить невозможно, так как жидкость всегда находится в сосуде, имеющем стенки. Однако, если размеры сосуда значительно превышают размеры шарика, то формулу (14) можно считать верной. В противном случае следует внести в формулу поправку, учитывающую радиус сосуда, в котором налита жидкость; для цилиндрического сосуда с учетом его радиуса расчетная формула примет вид:
Вопрос о том, какой формулой пользоваться, решается в зависимости от величины отношения r/R. Если оно меньше чем 0,05, то берут формулу (14), а если больше, то (15).
|


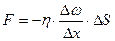 .
.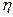 - коэффициент внутреннего трения (коэффициент вязкости),
- коэффициент внутреннего трения (коэффициент вязкости),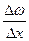 - градиент скорости, т. е. отношение изменение скорости к расстоянию, на котором оно осуществляются, взятом в направлении наибольшего возрастания скорости;
- градиент скорости, т. е. отношение изменение скорости к расстоянию, на котором оно осуществляются, взятом в направлении наибольшего возрастания скорости;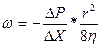 .
.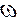 -скорость ламинарного течения жидкости;
-скорость ламинарного течения жидкости;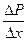 -градиент давления;
-градиент давления;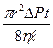
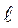
 -длина трубы
-длина трубы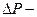 разность давлений на концах трубы;
разность давлений на концах трубы;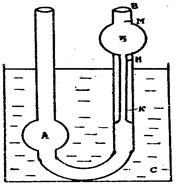
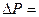

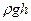
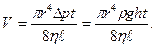
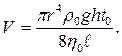
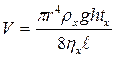
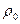 -плотность дистиллированной воды,
-плотность дистиллированной воды,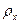 -плотность исследуемой жидкости,
-плотность исследуемой жидкости,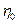 -коэффициент внутреннего трения воды,
-коэффициент внутреннего трения воды,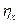 -коэффициент внутреннего трения жидкости,
-коэффициент внутреннего трения жидкости,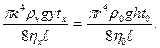
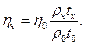
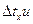
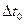 .
.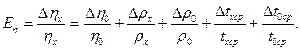
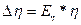
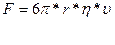
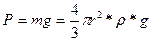
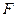 = 6πrηυ
= 6πrηυ