В произвольной точке плотины.
В первом приближении задаёмся функцией напряжений в виде следующего полинома φ(х, у) = где a, b, c, d – неизвестные постоянные коэффициенты. Получаем выражения напряжений
Постоянные a, b, c, d определяем из граничных условий
на вертикальной и наклонной гранях (рис. 2,а). На вертикальной грани x = 0, ℓ = cos(ν,x) = cos1800 = –1, m = cos(ν,y) = cos900 = 0, pν,x = γвy, pν,y = 0, σx = dy, σy = by, τxy = –cy условия (3) принимают вид
Отсюда d = –γв, c = 0 и выражения напряжений (2) можно записать следующим образом
На наклонной грани x = y∙tgβ, ℓ = cos(ν,x) = cosβ, m = cos(900 + β) = –sinβ, pν,x = pν,y = 0, σx = –γвy, σy = a y∙tgβ + by τxy = –by∙tgβ – γкy∙tgβ, поэтому условие (3) приводится к следующей системе уравнений
0 = –by∙tgβ∙cosβ – γкy∙tgβ∙cosβ + (a y∙tgβ + by)(– sinβ)
или
a tgβ + 2b + γк = 0 Решая систему получаем b = γвctg2β – γк a = –2γвctg3β + γкctgβ С учетом найденных величин a, b, c, d приводим выражения (2*) к виду
Выполняем проверку выражений компонентов напряженного состояния. Дифференцируем зависимости (4)
Подставляя полученные величины производных в уравнения равновесия
0 + 0 = 0 –γвctg2β + γвctg2β – γк + γк = 0 убеждаемся, что найденные выражения компонентов напряженного состояния в произвольной точке плотины, удовлетворяют этим уравнениям. Дважды дифференцируем зависимости (4)
Подставляем вторые производные в уравнение совместности
= Выражения названных компонентов удовлетворяют уравнению совместности деформаций в напряжениях. В окрестности произвольной точки Сна оси упри х = 0выделяем малый прямоугольный элемент единичной толщины (рис. 26). Напряжения в этой точке σх = –γву, σу = (γвctg2β – γк)y, τxy = 0 внешняя гидростатическая нагрузка Ρνx = γву Составляем уравнения равновесия выделенного элемента ΣXί = 0, Ρνx1dy – σx1dy = 0, γву – γву = 0, ΣYί = 0, σy1dx – σy1dx = 0, из которых видно, что найденные напряжения удовлетворяют условиям на поверхности вертикальной грани. Рассматриваем малый треугольный элемент в окрестности произвольной точки Dнаклонной грани плотины при x = y∙tgβ (pиc.2в). Напряжения в указанной точке σx = –γby σy = –γвy∙ctg2β τxy = –γвy∙ctgβ внешняя нагрузка отсутствует. Уравнения равновесия элемента ΣXί = 0, σx1dy – τyx1dx = 0, ΣYί = 0, τxy1dy – σy1dx = 0. или γвy∙dy – γвy∙ctgβ∙dx = 0, γвy∙ctgβ∙dy – γвy∙ctg2β∙dx = 0, или 1 – 1 – т.к. 1 – tgβ∙ctgβ = 0, 1 – 1 = 0, 1 – tgβ∙ctgβ = 0, 1 – 1 = 0 и, следовательно, найденные напряжения удовлетворяют условиям на поверхности наклонной грани. Дальнейшая корректировка выражений (4) для компонентов напряженного состояния не требуется, поскольку они удовлетворяют дифференциальным уравнениям равновесия, уравнению совместности деформаций и граничным условиям.
|

 , (1)
, (1)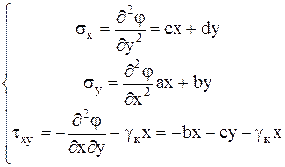 (2)
(2) (3)
(3) (3)
(3) (2*)
(2*) 0 = –γвy∙cosβ – by∙tgβ(– sin β) –γкy∙tgβ(– sin β)
0 = –γвy∙cosβ – by∙tgβ(– sin β) –γкy∙tgβ(– sin β) –γвctg2β + b + γк = 0
–γвctg2β + b + γк = 0 (4)
(4)
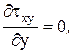




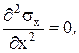
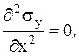


 2(σх + σу) =
2(σх + σу) = 
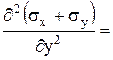
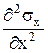 +
+ 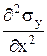 +
+ 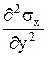 +
+  ctgβ = 0,
ctgβ = 0,


