МЕТОДИЧЕСКИЕ УКАЗАНИЯ. Утверждено редакционно-издательским советом
С.Н.Федотов
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ ИССЛЕДОВАНИЕ НАПРЯЖЕННОГО СОСТОЯНИЯ ПЛОТИНЫ ТРЕУГОЛЬНОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
Утверждено редакционно-издательским советом университета в качестве методических указаний по выполнению расчетно-графической работы
Санкт-Петербург УДК 539.3/.6 ББК 30.121 Рецензент Доктор технических наук, профессор В.Б. Чистов.
Сопротивление материалов (часть III. «Основы теории упругости и пластичности»). Исследование напряженного состояния плотины треугольного поперечного сечения: Методические указания по выполнению расчетно-графической работы. /составитель: С.Н.Федотов - СПб.: СПГУВК, 2009.-29с.
Приведены задания по выполнению расчетно-графической работы по дисциплине «Сопротивление материалов», методические указания по их выполнению и примеры расчетов. Предназначены для студентов очной и заочной форм обучения по специальности 270104.65 «Гидротехническое строительство».
УДК 539./.6 ББК 30.121 ©Санкт-Петербургский государственный Университет водных коммуникаций, 2009 С О Д Е Р Ж А Н И Е
Контрольные задания на выполнение работы ……………….. 4 План исследования ………………………………………………. 4 Методические указания ……………………………………....... 5 Пример выполнения работы…………………………………… 14 Контрольное задание………………………………………… 14 Исследование напряженного состояния плотины …..………….. 14 1. Отыскание компонентов напряженного состояния в произвольной точке плотины…………….. 14 2. Расчет напряжений ……………………………………… 20 3. Построение линий равных напряжений ………………… 23 4. Построение сетки траекторий главных напряжений…….. 26 5. Построение эллипсов напряжений……………………….. 26 Библиографический список…………………………………….. 29 КОНТРОЛЬНЫЕ ЗАДАНИЯ НА ВЫПОЛНЕНИЕ РАБОТЫ Исследовать по приведенному ниже плану напряженное состояние плотины треугольного профиля, которая испытывает плоскую деформацию в поперечном направлении под действием гидростатического давления на вертикальную грань и объемной нагрузки от собственного веса (рис.1). Для расчета нагрузок и напряжений заданы высота Н, угол β при гребне, объемный вес γк бетонной кладки тела плотины, объемный вес γв воды и уровень ее свободной поверхности. План исследования 1. Найти зависимости компонентов напряженного состояния от координат хи у произвольной точки тела плотины, используя полуобратный метод решения плоской задачи теории упругости в напряжениях. 2. Выполнить с помощью найденных зависимостей расчеты компонентов тензора напряжений σх, σу, τху, показать их эпюры в основании профиля и на его средней горизонтальной линии. 3. Построить линии равных главных напряжений σmin, σmaх и линии равных наибольших касательных напряжений │τmax│ возникающих на площадках перпендикулярных плоскости хоу. 4. Вычислить в характерных точках углы наклона главных напряжений и построить сетку их траекторий в поперечном сечении плотины. 5. Представить в масштабе эллипсы напряжений в средней и крайних точках основания профиля.
Рис. 1. Схема профиля плотины а)
б) в)
Рис.2. Граничные условия Исходные данные взять из таблицы 1 в соответствии с шифром (номером зачетной книжки студента). Значения Н и β выписать из строки, номер которой в таблице 1 совпадает с последней цифрой в шифре, а величину γк – из строки с номером, соответствующим предпоследней цифре шифра. Принять γв = 10 кн/м3. Таблица 1 Исходные данные
МЕТОДИЧЕСКИЕ УКАЗАНИЯ 1. В первом приближении задаться функцией напряжений в виде следующего полинома φ(х, у) = где a, b, c, d – неизвестные постоянные коэффициенты. Использовать соотношения σх = и найти из них с помощью зависимости (1) выражения напряжений через переменные х, у постоянные a, b, c, d. Определить величины a, b, c, d из граничных условий
на вертикальной и наклонной гранях, где ν - внешняя нормаль к контуру профиля в рассматриваемой точке; ℓ‚ m‚ n – направляющие конусы внешней нормали ν; Ρνх, Ρνу - составляющие внешней поверхностной нагрузки по осям координат в данной точке (рис. 2,а). Подставить найденные величины коэффициентов в выражения напряжений и получить расчетные зависимости для вычисления σх, σу,τху. Проверить удовлетворяют ли найденные зависимости дифференциальным уравнениям равновесия, уравнению совместности и граничным условиям. Привести в работе выкладки, подтверждающие, что уравнения равновесия
и уравнение совместности деформаций в напряжениях
обращаются в тождества при подстановке в них найденных выражений напряжений. Для проверки выполнения граничных условий рекомендуется, не прибегая к выражениям (3), показать, что напряжения σх, σу,τху при х = 0отвечают нагрузке на вертикальную грань и при х = у tgβ - отсутствию нагрузки на наклонной грани, рассмотрев равновесие прямоугольного элемента, вырезанного у вертикальной и треугольного - у наклонной грани (рис. 2б, 2в). Завершить проверку выводом о том, требуется корректировка выражений для напряжений в последующих приближениях или нет. Если нет, то приступить к вычислениям по этим выражениям. 2. Расчеты напряжений следует выполнять в точках, которые лежат на лучах, выходящих из вершины профиля и разделяющих его основание на ряд равных отрезков. В учебных целях достаточно провести пять лучей с номерами i = 0, l, 2, 3, 4,возрастающими слева направо так, чтобы нулевой луч прошел по вертикальной, а четвертый – по наклонной границам профиля. В этом случае между координатами произвольной точки, лежащей на любом из пяти лучей с номером i, имеет место соотношение Xi = с помощью которого целесообразно исключить переменную x из расчетных зависимостей для напряжений и записать выражения σх, σу,τху в таблицу 2 в виде линейных функций одного аргумента yдля каждого луча, как показано ниже в примере выполнения РПР. Получить в таком же виде выражения главных и максимальных касательных напряжений, возникающих на площадках перпендикулярных плоскости хоу. Использовать для этого формулы
σmin =
|τ|max = и поместить результаты расчета в таблицу 2. Выражения напряжений в таблице 2 должны быть проверены. В частности необходимо проверить выполняется ли закон постоянства суммы нормальных напряжений σx + σy = σmax + σmin (10) Убедиться также, что на втором луче σy = – 0,5γку, на четвертом σmax = 0, а σmin принимает наибольшее по абсолютной величине значение в точке В, и подготовить устное объяснение этих трех результатов. По данным таблицы 2 вычислить σx, σy, τху при у = Н/2, у = Ни построить эпюры перечисленных напряжений. 3. Линии равных напряжений рекомендуется строить в количестве nне менее 5 и не более 10 для каждого из трех семейств кривых σmin,σmax,|τxy|max. При построении линий первого семейства следует составить таблицу 3, образец которой приведен ниже в примере выполнения РПР. В первом столбце таблицы записать nзначений σmin,последовательно возрастающих по абсолютной величине приблизительно до ее максимума с равномерным предварительно вычисленным шагом
и округленным затем до ближайшего к нему меньшего числа кратного 50 кПа или 100 кПа. Первым в столбец заносится значение σmin = Δ σmin,последним – значение σmin = nΔ σmin. Например, если наибольшее сжимающее напряжение в плотине σmin = –2457 κΠа, а max |σmin| = 2457 кПаи решено построить 6линий равных напряжений этого вида, то шаг без округления Δ σmin = после округления Δ σmin = 400 кПа и значит в таблицу нужно записать 6 следующих значений σmin: –400, –800, –1200, –1600, –2000, –2400 кПа Следует обратить внимание на то, что при σmin= 0 линия равных минимальных напряжений вырождается в точку 0на вершине профиля плотины, а при σmin= –2457 кПа - в крайнюю правую точку Воснования. После заполнения столбца 1 нужно вычислить значения координаты удля точек пересечения линий равных напряжений σminскаждым лучом и занести в следующие пять столбцов таблицы 3. Вычисления произвести путем деления записанных в первый столбец этой таблицы напряжений на взятые из таблицы 2 множители при ув выражениях σmin. По данным таблицы 3 вычертить линии равных напряжений σmin. Построить таким же образом линии равных напряжений σmаx, |τ|max, предварительно составив и заполнив таблицу 4 и таблицу 5, подобные таблице 3. 4. Воспользоваться определением: траектория главного напряжения – линия, в каждой точке которой вектор, изображающий такое напряжение, касателен к этой линии. Сделать отсюда вывод, что для построения сетки траекторий нужно предварительно вычислить в ряде точек на лучах значения угла αнаклона главного напряжения σmаx к оси xи использовать для этого формулу
Достаточно определить пять значений: α0, α1, α2, α3, α4, подставляя поочередно в формулу (12) данные таблицы 2 для каждого луча. Эти же углы будут для главного напряжения σmin к оси Y. Убедиться, что для всех точек одного и того же луча значение αпостоянно и поэтому все лучи, исходящие из вершины профиля, представляют собой изоклины. Учесть, что вертикальная грань плотины является главной площадкой поскольку здесь τху = 0,а потому на нулевом луче расчет по формуле (12) приводит к одному из двух возможных результатов: 1) при σх – σmin ≠ 0 tgα0 = 0,откуда α0 = 0; 2) при σх – σmin = 0 tgα0 = ∞,откуда α0 = 90. Причем второй результат получается путем раскрытия неопределенности вида ø/ø. Таким образом в любой точке нулевого луча σmаxнаправлено либо вертикально, либо горизонтально. Учесть также, что и наклонная грань является главной площадкой, на которой σmаx = 0, а поэтому на четвертом луче искомый угол α4 = β. При построении траекторий нужно изобразить в масштабе профиль плотины со всеми лучами, а рядом вычертить углы α0, α1, α2, α3, α4 с общей вершиной и общей горизонтальной стороной, чтобы иметь пучок прямых в пяти направлениях σmаx. В учебных целях достаточно четырех–пяти траекторий для каждого из двух главных напряжений. В этом случае на второй луч нужно нанести три точки, разделяющие его на четыре равных участка между вершиной и основанием профиля. Чтобы построить одну траекторию σmаxследует через любую из этих точек, например, через среднюю провести под углом α2 к горизонтали отрезок так называемого второго направления путем параллельного переноса последнего с пучка прямых. Левый конец этого отрезка ограничить точкой, лежащей посередине между вторым и первым, а правый – посередине между вторым и третьем лучами. От левого конца отрезка второго направления таким же способом отложить под углом α1отрезок первого направления до середины между первым и нулевым лучом, а из правого конца под углом α3 - отрезок третьего направления до середины между третьим и четвертым лучами. Из левого конца отрезка первого направления провести крайний левый участок траектории σmаxперпендикулярно нулевому лучу, если α0 = 0,или в виде асимптоты к оси у, если α0 = 900.Крайний правый ее участок провести из правого конца отрезка третьего направления под углом α4= β т.е. перпендикулярно четвертому лучу. После этого нужно перейти к следующей точке на втором луче, получить подобным образом ещё одну траекторию σmаxи т.д., включая точку пересечения этого луча с основанием профиля. Далее следует построить на том же чертеже траектории σminописанным выше способом, предварительно изобразив для этих напряжений пучок их направлений перпендикулярных направлениям σmаx. Построения нужно начинать с тех же точек на втором луче и откладывать отрезки второго, первого, третьего и других направлений посредством параллельного переноса последних с этого пучка. Убедиться, что в полученной сетке траекторий нулевой и четвертый лучи также являются траекториями главных напряжений. 5. Чтобы вычертить эллипс напряжений в заданной точке луча, нужно наметить два пересекающихся в ней взаимно перпендикулярных направления σminи σmаxперенеся их, например, с изображений пучков. Затем отложить от неё по этим направлениям в противоположные стороны по два равных отрезка, представляющих в выбранном масштабе величины σminи σmаxв этой точке и являющиеся полуосями эллипса. После этого провести эллипс по четырем вершинам. Обратить внимание на то, что на четвертом луче эллипс вырождается в отрезок, а на нулевом луче большая ось эллипса располагается вертикально или горизонтально в зависимости от величины угла β. Подготовить устное объяснение таких особенностей эллипсов напряжений. 6. Работу представить в сброшюрованном виде на бумаге формата А4 с титульным листом установленного образца. В работе письменно сформулировать задание на её выполнение, изобразить схему профиля (рис.1), указать шифр и выбранные в соответствии с ним исходные данные, изложить теоретические выкладки и расчеты, иллюстрировать граничные условия задачи, как показано на рис.2, привести восемь итоговых графиков: 1) эпюры σх,2) эпюры σу,3) эпюры τху, 4) линии равных σmin, 5) линии равных σmаx,6) линии равных |τ |max, 7) траектории σmin, σmаx, 8) эллипсы напряжений. Каждый график построить на отдельно вычерченном для него профиле плотины в удобном при пользовании стандартном масштабе. Построения рекомендуется выполнять на миллиметровой бумаге указанного выше формата. На графиках нанести числовые значения напряжений. Допускается совмещение сетки траекторий σmin,σmаxи эллипсов напряжений на одном чертеже профиля. Студентам-заочникам разрешается оформление работы, включая построение графиков, в отдельной школьной тетради из бумаги в клетку.
|




 , (1)
, (1) ; σу =
; σу =  ; τху = –
; τху = – 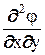 – γкх (2)
– γкх (2)
 (3)
(3) (4)
(4) 2(σх+σу) = 0 (5)
2(σх+σу) = 0 (5) ytgβ, (6)
ytgβ, (6) (7)
(7) (8)
(8) (9)
(9) (11)
(11) = 409,5 кПа
= 409,5 кПа (12)
(12)


