Методология функционального моделирования IDEF0

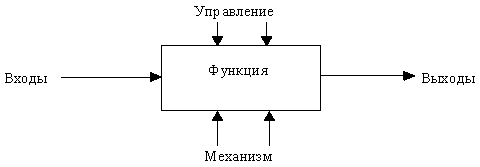
Описание системы с помощью IDEFO называется функциональной моделью. Функциональная модель предназначена для описания существующих бизнес-процессов, в котором используются как естественный, так и графический языки. Для передачи информации о конкретной системе источником графического языка является сама методология IDEFO.

Методология IDEFO предписывает построение иерархической системы диаграмм – единичных описаний фрагментов системы. Сначала проводится описание системы в целом и ее взаимодействия с окружающим миром (контекстная диаграмма), после чего проводится функциональная декомпозиция – система разбивается на подсистемы и каждая подсистема описывается отдельно (диаграммы декомпозиции). Затем каждая подсистема разбивается на более мелкие и так далее до достижения нужной степени подробности.

Каждая IDEFO-диаграмма содержит блоки и дуги (стрелки). Блоки изображают функции моделируемой системы. Дуги связывают блоки вместе и отображают взаимодействия и взаимосвязи между ними.

Функциональный блок графически изображается в виде прямоугольника и олицетворяет собой некоторую конкретную функцию в рамках рассматриваемой системы. Блок показывает, как входная информация трансформируется в выходной продукт, с помощью чего или кого и что регламентирует выполнение функции.

Каждый функциональный блок в рамках единой рассматриваемой системы должен иметь свой уникальный идентификационный номер, который присваивается автоматически. Все блоки должны быть названы и определены. Имя блока должно отражать действие и задается только в виде глагола, например, ИЗГОТОВИТЬ ДЕТАЛЬ, СОБРАТЬ ДАННЫЕ.

При создании новой модели автоматически создается контекстная диаграмма с единственным функциональным блоком, отображающим систему в целом (рисунок 1). На контекстной диаграмме кроме блока со стрелками в левом нижнем углу пишется цель выполнения работы и точка зрения, с которой рассматривается моделируемый процесс.

 

Рисунок 1 - Пример контекстной диаграммы

 

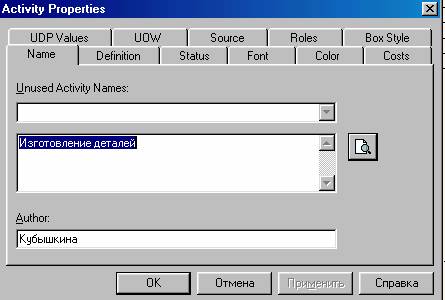
Для того чтобы задать другие свойства блока необходимо нажать правой клавишей мыши на изображении блока и выбрать нужное свойство «Activity properties» (рисунок 2).

Рисунок 2 - Редактор задания свойств работы

 

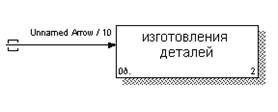
Второй основной элемент IDEF0–методологии — это стрелка. Стрелка бывает четырех типов: стрелка–вход, выход, механизм и управление.

1. Вход (Input) рисуется, как входящая в левую грань функционального блока. Вход показывает, что требуется для выполнения функции, например, СВЕДЕНИЯ О КЛИЕНТЕ, ЗАГОТОВКА.

2. Выход (Output) – исходящая из правой грани блока. Выход — результат функции, например, ГОТОВАЯ ДЕТАЛЬ, ОТЧЕТ.

3. Механизм (Mechanism) входящая в нижнюю грань стрелка. Механизм с помощью чего или кого выполняется функция, например, СОТРУДНИК, КОМПЬЮТЕР.

4. Управление (Control) рисуется входящей в верхнюю грань блока. Управление ограничивает (регламентирует) выполнение функции), например, УСТАВ, ГОСТы.

Также существует пятый тип стрелки — это стрелка вызова, которая носит технический характер и служит для слияния и расщепления моделей. Стрелка вызова рисуется также как стрелка–механизма, но имеет противоположное направление. Имена вновь внесенных стрелок автоматически заносятся в словарь (Arrow Dictionary).

Стрелки могут быть внутренними и граничные. Внутренние стрелки соединяют блоки между собой. Граничные стрелки служат для описания взаимодействия с внешней средой. Они могут начинаться у блока, а заканчиваться у границы диаграммы (на контекстной диаграмме используются только граничные стрелки).

Для внесения граничной стрелки надо:

· Щелкнуть по кнопке с символом стрелки в палитре инструментов, затем следует перенести курсор к левой стороне экрана, пока не появится начальная штриховая полоска;

· Щелкнуть один раз по полоске (откуда выходит стрелка) и еще раз в левой части блока со стороны входа (где заканчивается стрелка);

· Вернуться в палитру инструментов и выбрать опцию редактирования стрелки

· Щелкнуть правой кнопкой мыши на линии стрелки, во всплывающем меню выбрать Name и добавить имя стрелки в закладке Name диалога Arrow Properties.

Разветвляющиеся и сливающиеся стрелки. Одни и те же данные или объекты, порожденные одним процессом, могут использоваться сразу в нескольких других процессах. С другой стороны, стрелки, порожденные в разных работах, могут представлять собой одинаковые или однородные данные или объекты, которые в дальнейшем используются или перерабатываются в одном месте.

Для моделирования таких ситуаций в IDEF0 используются разветвляющиеся и сливающиеся стрелки. Для разветвления стрелки нужно в режиме рисования стрелки щелкнуть по фрагменту стрелки и по соответствующему сегменту блока. Для слияния двух стрелок выхода нужно в режиме рисования стрелки сначала щелкнуть по сегменту выхода блока, а затем по соответствующему сегменту стрелки.

Существуют определенные правила именования таких стрелок. Если стрелка именована до разветвления, а после разветвления ни одна из ветвей не именована, то подразумевается, что каждая ветвь моделирует те же данные или объекты, что и ветвь до разветвления. Если стрелка именована до разветвления, а после разветвления какая-либо из ветвей, то подразумевается, что именованная ветвь моделирует данные соответствующие ее имени, а не именованная те же данные, что и ветвь до разветвления. Недопустима ситуация, когда стрелка до разветвления не именована, и после разветвления не именована какая-либо из ветвей. BPWin 4.0 определяет такую стрелку как синтаксическую ошибку. Правила именования сливающихся стрелок аналогичны.

Туннелирование стрелок. Вновь внесенные граничные стрелки на диаграмме декомпозиции нижнего уровня изображаются в квадратных скобках и автоматически не появляются на диаграмме верхнего уровня. Квадратный туннель является предупреждением для разработчика о возможной ошибке (случайное удаление или добавление стрелки). Квадратный туннель должен быть заменен на круглый туннель либо стрелка добавлена на родительской диаграмме.

Рисунок 3 - Неразрешенная стрелка

Для их «перетаскивания» наверх нужно щелкнуть правой кнопкой мыши по квадратным скобкам граничной стрелки и выбрать из выпадающего меню Arrow Tunnel. Появится диалоговое окно Border Arrow Editor.

 

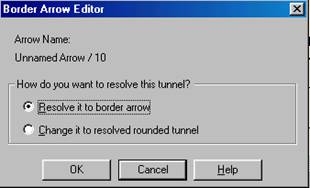
Рисунок 4 - Диалог Border Arrow Editor

 

Если выбрать resolve it to border arrow, то стрелка мигрирует на диаграмму верхнего уровня. Если выбрать Change it to resolve rounded tunnel, то стрелка будет затуннелирована и не попадет на другую диаграмму. Тоннельная стрелка изображается с круглыми скобками на конце. Туннелирование может быть применено для изображения малозначимых стрелок. Если на какой-либо диаграмме нижнего уровня необходимо изобразить малозначимые данные или объекты, которые не обрабатываются или не используются процессами на текущем уровне, то их необходимо направить на вышестоящий уровень (родительскую диаграмму).

Если эти данные не используются на родительской диаграмме их надо направить еще выше, и так далее. В результате малозначимая стрелка будет изображена на всех уровнях и затруднит чтение всех диаграмм, на которых она присутствует. Выходом является туннелирование стрелки на самом нижнем уровне. Такое туннелирование называется «не-в-родительской-диаграмме».

Другим примером туннелирования может быть ситуация, когда стрелка механизма мигрирует с верхнего уровня на нижний, причем на нижнем уровне этот механизм используется одинаково во всех процессах без исключения. В этом случае стрелка механизма на нижнем уровне может быть удалена, после чего на родительской диаграмме она может быть затуннелирована, а в комментарии к стрелке указать, что механизм будет использоваться во всех процессах дочерней диаграммы декомпозиции. Такое туннелирование называется «не-в-дочерней-работе».