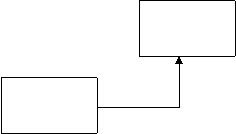Создание иерархии диаграмм

Для создания диаграммы декомпозиции следует щелкнуть по кнопке . Появится окно диалога Activity Box Count, в котором следует указать методологию новой диаграммы и количество функциональных блоков на ней.

 

Рисунок 5 - Диалог Activity Box Count

 

Для создания дополнительных блоков нужно нажать на кнопку и указать расположение блока.

Функциональные блоки автоматически нумеруются в соответствии со значением параметра Numbering (Нумерация), установленным в разделе Model Properties в меню Model. Номер блока записывается в правом нижнем углу блока.

IDEFO требует, чтобы в диаграмме было не менее трех и не более шести блоков. Эти ограничения поддерживают сложность диаграмм и модели на уровне, доступном для чтения, понимания и использования.

Блоки в IDEFO размещаются по степени важности, как ее понимает автор диаграммы. Этот относительный порядок называется доминированием. Доминирование понимается как влияние, которое один блок оказывает на другие блоки диаграммы. Например, самым доминирующим блоком диаграммы может быть либо первый из требуемой последовательности функций, либо планирующая или контролирующая функция, влияющая на все другие.

Наиболее доминирующий блок обычно размещается в верхнем левом углу диаграммы, а наименее доминирующий – в правом углу.

Расположение блоков на странице отражает авторское определение доминирования. Таким образом, топология диаграммы показывает, какие функции оказывают большее влияние на остальные. Чтобы подчеркнуть это, аналитик может перенумеровать блоки в соответствии с порядком их доминирования. Порядок доминирования может обозначаться цифрой, размещенной в правом нижнем углу каждого прямоугольника: 1 будет указывать на наибольшее доминирование, 2 – на следующее и т. д.

В методологии IDEFO требуется только пять типов взаимодействий между блоками для описания их отношений: вход (рисунок 6), управление (рисунок 7), обратная связь по входу (рисунок 8), обратная связь по управлению (рисунок 9), выход-механизм (рисунок 10). Связи по управлению и входу являются простейшими, поскольку они отражают прямые воздействия, которые интуитивно понятны и очень просты.

Рисунок 6 – Связь по входу

 

Отношение управления возникает тогда, когда выход одного блока непосредственно влияет на блок с меньшим доминированием.

 

Рисунок 7 – Связь по управлению

 

Обратная связь по управлению и обратная связь по входу являются более сложными, поскольку представляют собой итерацию или рекурсию. А именно выходы из одной работы влияют на будущее выполнение других работ, что впоследствии повлияет на исходную работу.

Рисунок 8 – Обратная связь по входу

 

Обратная связь по управлению возникает тогда, когда выход некоторого блока влияет на блок с большим доминированием.

 

Рисунок 9 – Обратная связь по управлению

 

Связи «выход-механизм» встречаются нечасто. Они отражают ситуацию, при которой выход одной функции становится средством достижения цели для другой.

Связи «выход-механизм» характерны при распределении источников ресурсов (например, требуемые инструменты, обученный персонал, физическое пространство, оборудование, финансирование, материалы).

Рисунок 10 – Связь выход-механизм

 

В IDEFO дуга редко изображает один объект. Обычно она символизирует набор объектов. Так как дуги представляют наборы объектов, они могут иметь множество начальных точек (источников) и конечных точек (назначений). Поэтому дуги могут разветвляться и соединяться различными способами. Вся дуга или ее часть может выходить из одного или нескольких блоков и заканчиваться в одном или нескольких блоках.

Разветвление дуг, изображаемое в виде расходящихся линий, означает, что все содержимое дуг или его часть может появиться в каждом ответвлении. Дуга всегда помечается до разветвления, чтобы дать название всему набору. Кроме того, каждая ветвь дуги может быть помечена или не помечена в соответствии со следующими правилами:

· непомеченные ветви содержат все объекты, указанные в метке дуги перед разветвлением;

· ветви, помеченные после точки разветвления, содержат все объекты или их часть, указанные в метке дуги перед разветвлением.

Слияния дуг в IDEFO, изображаемое как сходящиеся вместе линии, указывает, что содержимое каждой ветви идет на формирование метки для дуги, являющейся результатом слияния исходных дуг. После слияния результирующая дуга всегда помечается для указания нового набора объектов, возникшего после объединения. Кроме того, каждая ветвь перед слиянием может помечаться или не помечаться в соответствии со следующими правилами:

· непомеченные ветви содержат все объекты, указанные в общей метке дуги после слияния;

· помеченные перед слиянием ветви содержат все или некоторые объекты из перечисленных в общей метке после слияния.