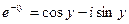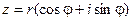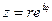КОМПЛЕКСНЫЕ ЧИСЛА
Рассмотрим показательную функцию Можно показать, что функция w может быть записана в виде:
Данное равенство называется уравнением Эйлера.
Для комплексных чисел будут справедливы следующие свойства:
1) 2) 3)
Если в уравнении Эйлера показатель степени принять за чисто мнимое число (х=0), то получаем:
Для комплексно – сопряженного числа получаем:
Из этих двух уравнений получаем:
Этими формулами пользуются для нахождения значений степеней тригонометрических функций через функции кратных углов.
Если представить комплексное число в тригонометрической форме:
и воспользуемся формулой Эйлера:
Полученное равенство и есть показательная форма комплексного числа.
Контрольные вопросы: 1. Дайте определение комплексного числа. Раскройте геометрическое представление комплексного числа. Какова тригонометрическая форма комплексного числа? 2. Какие действия выполняются над комплексными числами? Охарактеризуйте каждое их них. 3. Назовите уравнение Эйлера. Где его применяют? Какова показательная форма комплексного числа? Литература: 1. Высшая математика для экономистов: Учебник для вузов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н.Фридман. Под ред. Н.Ш. Кремера. – М.: ЮНИТИ, 2005. – 471 с. 2. Общий курс высшей математики для экономистов: Учебник. / Под ред. В.И. Ермакова. –М.: ИНФРА-М, 2006. – 655 с. 3. Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред.В.И. Ермакова. М.: ИНФРА-М, 2006. – 574 с. 4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. 1, 2. – М.: Оникс 21 век: Мир и образование, 2005. – 304 с. Ч. 1; – 416 с. Ч. 2. 5. Математика в экономике: Учебник: В 2-х ч. / А.С. Солодовников, В.А. Бабайцев, А.В. Браилов, И.Г. Шандара. – М.: Финансы и статистика, 2006. 6. Шипачев В.С. Высшая математика: Учебник для студ. вузов – М.: Высшая школа, 2007. – 479 с.
КОМПЛЕКСНЫЕ ЧИСЛА
|

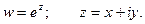

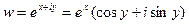


 где m – целое число.
где m – целое число.