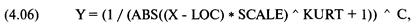Создание характеристической функции распределения

 

Нормальное распределение вероятности далеко не всегда является хорошей мо­делью распределения торговых прибылей и убытков. Более того, ни одно из рас­пространенных распределений вероятности не является идеальной моделью. По­этому мы должны сами создать функцию для моделирования распределения на­ших торговых прибылей и убытков.

Распределение изменений цены в общем случае относится к распределе­ниям Парето (см. приложение В). Распределение торговых P&L можно счи­тать трансформацией распределения цен. Эта трансформация является ре­зультатом торговых методов, когда трейдеры пытаются понизить свои убыт­ки и увеличить прибыли, следовательно, распределение торговых P&L можно отнести к распределениям Парето. Однако распределение, которое мы будем изу­чать, не является распределением Парето. Распределение Парето, как и все другие функции распределения, модели­рует определенное вероятностное явление. Оно моделирует распределение сумм независимых, идентично распределенных случайных переменных. Фун­кция распределения, которую мы будем изучать, не моделирует конкретное вероятностное явление. Она моделирует многие унимодальные функции рас­пределения. Поэтому она может повторить форму и плотность вероятности распределения Парето, а также любого другого унимодального распределения.

Теперь мы создадим эту функцию. Для начала рассмотрим следующее уравнение:

(4.02) Y=1/(X^ 2+1)

График этого уравнения — обычная колоколообразная кривая, симметрич­ная относительно оси Y, как показано на рисунке 4-2.

Таким образом, мы будем строить свои рассуждения, используя это общее уравнение. Переменную Х можно представить как число стандартных еди­ниц с каждой стороны от среднего, т.е. от оси Y. Мы можем использовать первый момент этого «распределения», расположение его среднего значения, добавив значение для изменения расположения на оси X. Уравнение изменится следую­щим образом:

(4.03) Y=1/(X-LOC^2+1),

где Y = ордината характеристической функции;

Х = количество стандартных отклонений;

LOC = переменная, задающая расположение среднего значения, первый момент распределения.

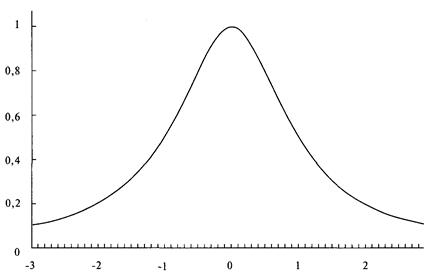
Рисунок 4-2 LOC = 0 SCALE = I SKEW = 0 KURT = 2

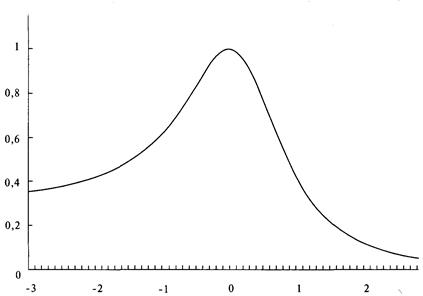
Рисунок 4-3 LOC =0,5, SCALE = 1, SKEW = 0, KURT= 2

 

Таким образом, если бы мы хотели изменить расположение, передвинув график влево на 0,5 единицы, мы бы установили LOC на -0.5. Этот график изображен на рисунке 4-3.

Таким же образом, если бы мы хотели сместить кривую вправо, то исполь­зовали бы положительное значение для переменной LOC. LOC с нулевым значением не будет смещать график, как показано на рисунке 4-2.

Показатель в знаменателе влияет на эксцесс. До настоящего момента экс­цесс был равен 2, но мы можем изменить его, изменив значение показателя. Те­перь формулу нашей характеристической функции можно записать следующим образом:

(4.04) Y = 1 / ((X - LOC)^ KURT + 1),

где Y == ордината характеристической функции;

Х = количество стандартных отклонений;

LOC = переменная, задающая расположение среднего значения, первый момент распределения;

KURT = переменная, задающая эксцесс, четвертый момент распределения.

Рисунки 4-4 и 4-5 показывают влияние эксцесса на нашу характеристическую функцию. Отметьте: чем выше показатель, тем более плосковерхое и тонкохвостое распределение (эксцесс меньше нормального), и чем меньше показа­тель, тем более острый верх и тем толще хвосты распределения (эксцесс боль­ше нормального). Чтобы не получить иррациональное число, когда KURT < 1, мы будем исполь­зовать абсолютное значение коэффициента в знаменателе. Это не повлияет на форму кривой. Таким образом, мы можем переписать уравнение (4.04) следую­щим образом:

(4.04) Y = 1/(ABS(X - LOC)^ KURT + 1)

Мы можем добавить множитель в знаменателе, чтобы контролировать шири­ну, второй момент распределения. Характеристическая функция будет выглядеть следующим образом:

(4.05) Y = 1 / (ABS((X - LOC) * SCALE)^ KURT + 1),

где Y = ордината характеристической функции;

X = количество стандартных отклонений;

LOC = переменная, задающая расположение среднего значения, первый момент распределения;

 

Рисунок 4-4 LOC=0, SCALE =1, SKEW = 0, KURT = 3

Рисунок 4-5 LOG = 0, SCALE = 1, SKEW = О, KURT = 1

 

KURT = переменная, задающая эксцесс, четвертый момент распределения;

SCALE = переменная, задающая ширину, второй момент распределения.

Рисунки 4-6 и 4-7 иллюстрируют изменение параметра ширины. Действие этого параметра можно представить как движение горизонтальной оси вверх или вниз Когда ось сдвигается вверх (при уменьшении ширины), график расширяется (см рисунок 4-6), как будто мы смотрим на его верхнюю часть. На рисунке 4-7 показа­на обратная ситуация, когда горизонтальная ось сдвигается вниз и кривая распре­деления сжимается. Теперь у нас есть характеристическая функция распределения, с помо­щью которой мы контролируем три из четырех моментов распределения Сейчас распределение симметрично. Для этой функции нам необходимо до­бавить коэффициент асимметрии, третий момент распределения. Характе­ристическая функция тогда будет выглядеть следующим образом:

где С = показатель асимметрии, рассчитанный следующим образом:

Y = ордината характеристической функции;

Х= количество стандартных отклонений;

LOC= переменная, задающая расположение среднего значения, первый момент распределения;

KURT = переменная, задающая эксцесс,

четвертый момент распределения;

SCALE = переменная, задающая ширину, второй момент распределения;

SKEW= переменная, задающая асимметрию, третий момент распределения;

sign() = функция знака, число 1 или -1. Знак Х рассчитывается как X/ ABS(X) для X, не равного 0. Если Х равно нулю, знак будет счи­таться положительным;

Рисунки 4-8 и 4-9 показывают действие переменной асимметрии на распре­деление. Отметим несколько важных особенностей параметров LOC, SCALE, SKEW и KURT. За исключением переменной LOC (которая выражена как число стандартных значений для смещения распределения), другие три

 

Рисунок 4-6 LOC=0, SCALE =0,5, SKEW = 0, KURT=2

Рисунок 4-7 LOC=0, SCALE = 2, SKEW = 0, KURT=2,

Рисунок 4-8 LOC=0, SCALE =1, SKEW =-0,5, KURT = 2.

Рисунок 4-9 LOG = 0, SCALE = 1, SKEW = +0,5, KURT = 2.

 

переменные являются безразмерными, то есть их значения являются числами, ко­торые характеризуют форму распределения и относятся только к этому рас­пределению. Значения параметров будут другими, если вы примените стандартные измери­тельные методы, детально описанные в разделе «Величины, описывающие рас­пределения» главы 3. Например, если вы определите один из коэффициентов асимметрии Пирсона на наборе данных, он будет отличаться от значения пере­менной SKEW для распределений, рассматриваемых здесь. Значения четырех пе­ременных уникальны для рассматриваемого распределения и имеют смысл толь­ко в данном контексте. Крайне важен интервал возможных значений этих переменных. Переменная SCALE всегда должна быть положительной, кроме того, она не ограничена сверху. То же самое верно для переменной KURT. На практике, однако, лучше использовать значения от 0,5 до 3, в крайнем случае, от 0,05 до 5. Вы можете ис­пользовать значения и за пределами этих крайних точек при условии, что они больше нуля.

Переменная LOC может быть положительной, отрицательной или нулем. Па­раметр SKEW должен быть больше или равен -1, и меньше или равен +1. Когда SKEW равен +1, вся правая сторона распределения (справа от пика) равна пику. Когда SKEW равен -1, пику равна вся левая сторона распределения. Интервалы значений переменных в общем виде таковы:

(4.08) - бесконечность < LOC < + бесконечность

(4.09) SCALE > 0

(4.10) -1<=SKEW<=+1

(4.11) KURT > О

Рисунки с 4-2 по 4-9 показывают, как легко изменяется распределение. Мы мо­жем подогнать эти четыре параметра таким образом, чтобы получившееся в ре­зультате распределение было похоже на любое другое распределение.