Разложение функции алгебры логики по переменным. СДНФ, СКНФ. Полином Жегалкина.Разложение функции алгебры логики по переменным. СДНФ, СКНФ. Полином Жегалкина.
Логической степенью переменной х называется выражение
Другими словами, логическая степень – выражение, которое обозначает переменную или ее отрицание.
 . Данное утверждение можно пояснить табл.2.11.
На основании этого можно определить следующее общее свойство логической степени: xs= 1 тогда и только тогда, когда x=s (соответственно xs= 0Û x≠s). Рассмотрим набор переменных {x1,..,xn}. Конъюнкцией (дизъюнкцией) над множеством переменных {x1,..,xn} называетсялюбое выражение вида Рангом конъюнкции (дизъюнкции) над множеством переменных {x1,..,xn} называетсяколичество попарно различных переменных в конъюнкции (дизъюнкции). Пример. Рассмотрим набор переменных {x1,x2,x3,x4}. Тогда Конъюнкция (дизъюнкция) над множеством переменных {x1,..,xn} называется элементарной, если все переменные в ней попарно различны. Элементарную конъюнкцию (дизъюнкцию) над множеством переменных {x1,..,xn}, называют совершенной, если она имеет ранг n. Иными словами, совершенная конъюнкция (дизъюнкция) – это такая, в которой присутствуют все переменные из рассматриваемой совокупности, причем по 1 разу. Пример.
Конъюнкцию (дизъюнкцию) над множеством переменных {x1,..,xm} можно обозначать K(D) или Ki(Di). Дизъюнктивной (конъюнктивной) нормальной формой называется формула вида K1 Ú K2 Ú … Ú Kl или Пример.
Дизъюнктивная (конъюнктивная) нормальная форма называется совершенной дизъюнктивной(конъюнктивной) нормальной формой или СДНФ(СКНФ),если каждая конъюнкция (дизъюнкция) в ней является совершенной. Пример. Для набора переменных {x1,x2,x3} Теорема (о разложении функции алгебры логики по m переменным). Каждую функцию алгебры логики f(x1,..,xn) для любого m ≤ n следующее можно представить в следующей форме:
Доказательство. Подставим вместо переменных x1,..,xn любые конкретные значения a1,..,an ÎE2. Тогда в левой части равенства (2.1) получим f(a1,..,an), в правой Тогда рассматриваемое выражение можно преобразовать к виду
Тем самым равенство доказано. Следствие (разложение функции алгебры логики по всем переменным). Для любой функции алгебры логики, не тождественно равной 0, справедливо разложение:
Доказательство. В равенстве (2.1) положим m=n, получим:
Теорема позволяет функции с большим числом переменных выразить с помощью формул над функциями с меньшим числом переменных.
Пример.
Согласно (2.1), получим
По табл.2.12 функции f(x1,x2) определяем, что f принимает значение 1 на двух наборах (s1,s2) значений переменных – на наборах (0,0) и (1,1). Отсюда, согласно (2.2),
Теорема. Для любой функции алгебры логики, не тождественно равной 1, справедливо следующее разложение:
Доказательство. Докажем теорему, используя принцип двойственности.
|
, в котором 
Î{x1,..,xn}, j= 
.
(
) – конъюнкция (дизъюнкция) ранга 3.
– элементарная конъюнкция над множеством переменных {x1,x2,x3,x4}, но не совершенная; 
– совершенная конъюнкция над множеством переменных {x1,x2,x3,x4}.
(D1 &D 2 & … &D l или 
).
–дизъюнктивная нормальная форма. 
– конъюнктивная нормальная форма.
– совершенная дизъюнктивная нормальная форма,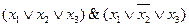 
– совершенная конъюнктивная нормальная форма.
. Выражение 
равно нулю, если существует i (1 ≤ i ≤ m), при котором ai≠si (по свойству логической степени и свойству конъюнкции x 
0=0).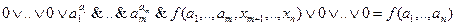
, так как
,а по свойству дизъюнкции 
. Мы видим,таким образом, что левая и правая части выражения (2.1) совпадают при подстановке вместо переменных любых значений.
.
.
– разложение по переменной x1.
– СДНФ для 
.
.
