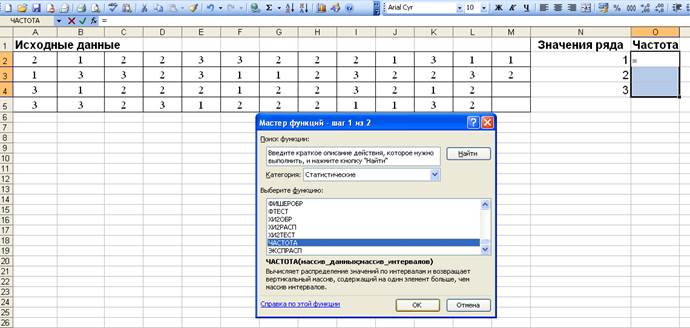
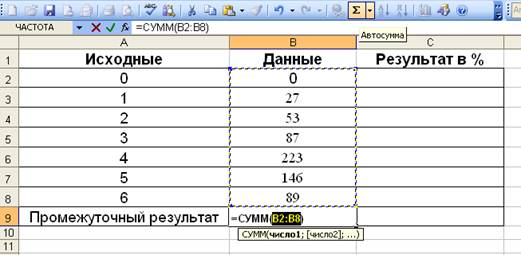
Обязательно нужно проверять сумму относительных частот! Она ВСЕГДА должна быть равна ЕДИНИЦЕ!

 

Таблицы:

1. Профессионально-значимые качества личности учителя.

2. Педагогическая культура учителя.

3. Педагогическая деятельность, ее структура.

 

2. Диагностические материалы по выявлению мотивации выбора педагогической профессии и направленности на профессию «человек - человек».

 

 

Лабораторная работа № 2

Математическая статистика

1. Сбор и группировка статистических данных. Частота

Для изучения различных общественных и социально-экономических явлений, а также некоторых процессов, происходящих в природе, проводятся статистические исследования. Любое статистическое исследование начинается с целенаправленного сбора информации об изучаемом явлении или процессе, называемом статистическим наблюдением.

Для обобщения и систематизации данных, полученных в результате статистического наблюдения, их по какому-либо признаку разбивают на группы и результаты группировки сводят в таблицы.

Пример 1. Администрация школы решила проверить математическую подготовку восьмиклассников. С этой целью был составлен тест, содержащий 9 заданий.

Работу выполняли 40 учащихся школы. При проверке каждой работы учитель отмечал число верно выполненных заданий. В результате был составлен такой ряд чисел

6. 5, 4, 0, 5, 7, 9, 1, 6, 8, 7, 9, 5, 8, 6, 7, 2, 5, 7, 6, 3, 4, 4, 5, 6, 8, 6, 7, 7, 4, 3, 5, 9, 6, 7, 8, 6, 9, 8

Для того, чтобы удобно было анализировать полученные данные, упорядочим этот ряд:

0, 1, 2, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, 6, 6, 7, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 9, 9, 9, 9.

Представим полученные данные в виде таблицы, в которой для каждого числа верно выполненных заданий, записанного в верхней строке, укажем в нижней строке количество появлений этого числа в ряду, то есть частоту.

Число верно выполненных заданий
Частота

Такую таблицу называют таблицей частот.

Сумма частот должна быть равна общему числу проверяемых работ! Проверить.

 

Обычно составляется не таблица частот, а таблица относительных частот. В таблице относительных частот для каждого числа верно выполненных заданий указывается не частота, а отношение частоты к общему числу данных в ряду (их всего 40). Это отношение и называют относительной частотой, а саму такую таблицу – таблицей относительных частот.

Число верно выполненных заданий
Частота
Относительная частота	0,025	0,025	0,025	0,05	0,125	0,15	0,2	0,175	0,125	0,1

Обязательно нужно проверять сумму относительных частот! Она ВСЕГДА должна быть равна ЕДИНИЦЕ!

 

Проанализировать результаты выполнения теста восьмиклассниками одной школы не так уж сложно. А если необходимо проверить математическую подготовку во всех школах города или региона? Организация такой проверки связана с серьёзными трудностями по пересылке тестов в школы, сбору и проверке работ, обработке полученных результатов. Вообще, любое массовое исследование требует больших организаторских усилий и финансовых затрат.

В тех случаях, когда бывает сложно или даже невозможно провести наблюдение над всеми объектами исследования (сплошное исследование), его заменяют выборочным.

При выборочном исследовании из всей изучаемой совокупности данных, называемых генеральной совокупностью, выбирается определенная ее часть, то есть составляется выборочная совокупность (выборка), которая подвергается исследованию. При этом выборка должна быть представительной, или, как говорят, репрезентативной, то есть отражающей характерные особенности исследуемой генеральной совокупности.

Пусть, например, в ходе кампании по выборам мэра в городе со стотысячным населением хотят узнать, кто из кандидатов имеет наибольшие шансы на успех. Для этого проводят опрос, например, полутора избирателей, в ходе которого выясняется, за которого они собираются голосовать. При этом нельзя опрашивать только молодых избирателей или только пенсионеров, так как это может привести к неправильным выводам Необходимо, чтобы среди опрашиваемых было примерно одинаковое число мужчин и женщин, людей с разным социальным положением, образованием и т.д.

Выборочное исследование проводят также тогда, когда проведение сплошного исследования связано с порчей или уничтожением продукции.

 

Задание 1. На выборах мэра города будут баллотироваться три кандидата:

1. Алексеев;

1. Иванов;
2. Карпов

(обозначим их 1, 2, 3). Проведя опрос 50 избирателей, выяснили, за кого из кандидатов они собираются голосовать. Получили следующие данные:

Представьте эти данные в виде таблицы частот.

 

Алгоритм действий:

1. выделяем диапазон, в котором должны быть рассчитанные частоты

1. выбираем статистическую функцию ЧАСТОТА

 

1. Выбираем в окне «массив данных» диапазон с исходными данными

 

1. выбираем в окне «массив интервалов» имеющиеся значения ряда

 

1. Нажимаем Ctrl+Shift+Enter (одновременно) вместо Enter

 

Задание 2. В ходе опроса 34 учащихся школы было выяснено, сколько времени в неделю (с точностью до 0,5 часа) они затрачивают не занятиях в кружках и спортивных секциях. Получили следующие данные:

	1,5		2,5
			2,5	3,5
		3,5	2,5
1,5	4,5
3,5		3,5		2,5
				4,5
	3,5

Представьте этот ряд в виде таблицы частот. Найдите, сколько времени тратят в среднем ученики на занятия в кружках и спортивных секциях.

 

Задание 3. Учащимся восьмых классов школы города N была предложена контрольная работа по алгебре, содержащая 6 заданий. При подведении итогов составили таблицу, в которой было указано число учащихся, верно выполнивших одно, два, три и т.д. задания

Число выполненных заданий	Число учащихся
	-

Пользуясь этой таблицей, составьте таблицу относительных частот, с точностью до 0,01.

Проверить, чтобы сумма относительных частот была равна единице! Посчитать в ячейке С9.

 

Задание 4. При проверке 70 работ по русскому языку отмечали число орфографических ошибок, допущенных учениками. Полученный ряд данных представили в виде таблицы частот:

Число ошибок
Частота

Каково наибольшее различие в числе допущенных ошибок? Какое число ошибок является наиболее типичным для данной группы учащихся? Укажите, какие статистические характеристики были использованы при ответе на поставленные задачи?

 

Задание 5. Ряд данных о количестве акций одинаковой стоимости, приобретенных сотрудниками лаборатории, представлен в виде таблицы частот

Число акций	Частота

Для этого ряда найдите среднее арифметическое, размах и моду. Что характеризует каждый из этих показателей?

Задание 6. При изучении качества продукции, выпущенной цехом, определяли число бракованных деталей в каждом из 50 произвольным образом выбранных ящиков с одинаковым числом деталей. Получили следующую таблицу

Число бракованных деталей
Число ящиков

Найдите среднее арифметическое, размах и моду полученного ряда данных. Объясните практический смысл этих статистических характеристик.

 

Задание 7. Определяя степень засоренности цветочных семян, выяснили, сколько семян сорных растений содержится в каждом из 100 произвольным образом выбранных пакетов с одинаковым числом семян. Получили следующую таблицу

Число семян сорных растений
Число пакетов

Для получения ряда данных найдите среднее арифметическое и моду полученного ряда данных. Объясните практический смысл этих характеристик.

 

Задание 8. При изучении учебной нагрузки 32 восьмиклассника попросили отметить время (с точностью до 0,1 ч), которое они затратили в определенный день на выполнение домашних заданий. Получили следующие данные

2,7	2,5	3,1	3,2	3,4	1,6	1,8	4,2
2,6	3,4	3,2	2,9	1,9	1,5	3,7	3,6
3,1	2,9	2,8	1,5	3,1	3,4	2,2	2,8
4,1	2,4	4,3	1,9	3,6	1,8	2,8	3,9

Пользуясь этой таблицей, составьте таблицу частот и таблицу относительных частот, с точностью до 0,01.