Теоретическое введение. Различают собственную и примесную проводимость полупроводников
Различают собственную и примесную проводимость полупроводников. При собственной проводимости плотность тока определяется выражением
где Используя закон Ома в дифференциальной форме
получим формулу удельной электропроводности собственного полупроводника
В полученном выражении Удельная электропроводность примесных полупроводников, обусловленная как собственными, так и примесными носителями (например, электронами), определяется выражением
Из уравнений (3) и (4) следует, что температурная зависимость электропроводности полупроводников определяется зависимостью от температуры концентрации собственных и примесных носителей и их подвижностью. Подвижность свободных носителей в кристалле определяется их рассеянием на неоднородностях кристаллической решетки. При низких температурах преобладает рассеяние на ионизированных примесных атомах. Рассеяние состоит в том, что ионы примеси отклоняют электроны, проходящие вблизи них, и тем самым уменьшают скорость их упорядоченного движения. Согласно расчетам при низких температурах
При высоких температурах основное значение имеет рассеяние электронов и дырок на тепловых колебаниях решетки, зависимость подвижности от температуры имеет вид
Рис. 1.
где С1 и С2 – константы слабо зависящие от температуры, Еg – энергия активации собственных носителей, ЕD – энергия активации донорной, либо акцепторной примеси. Таким образом, концентрация собственных и примесных носителей растет с повышением температуры по экспоненциальному закону. Если по оси абсцисс отложить 1/Т, а по оси ординат ln n,то эта зависимость будет иметь вид ломаной линии (рис.2).
Рис.2. Рис.3 Область АВ соответствует низким температурам. При этих температурах происходит постепенное возбуждение примесных носителей: электронов в полупроводниках с донорной примесью и дырок в полупроводниках с акцепторной примесью. При достижении температуры Тs все примесные атомы ионизируются и наступает истощение примесных носителей. Их концентрация становится равной концентрации примесей и, следовательно, не зависит от температуры (участок ВС). Температура истощения примеси тем выше, чем больше энергия активации примеси и ее концентрация. При дальнейшем повышении температуры начинается интенсивное возбуждение собственных носителей (участок СД). Температура перехода к собственной проводимости Тi тем выше, чем больше ширина запрещенной зоны Еg. Проанализируем теперь температурную зависимость электропроводности полупроводников, исходя из зависимости от температуры концентрации носителей и их подвижности. Схематически кривая зависимости Низкотемпературная область АВ отвечает примесной проводимости полупроводника, возникающей вследствие ионизации примесных атомов и появления примесных носителей. Подвижность носителей при этих температурах определяется рассеянием на ионизированных атомах примеси. В первом приближении этой зависимостью по сравнению с экспоненциальной можно пренебречь, считая что
где Логарифмируя (7), получим уравнение, описывающее прямую АВ
Тангенс угла наклона прямой АВ к оси абсцисс равен
Таким образом, по графику зависимости Область ВС простирается от температуры истощения примесных носителей TS до температуры перехода к собственной проводимости Тi. В этой области все примесные атомы ионизированы, но еще не происходит заметного возбуждения собственных носителей, вследствие чего концентрация носителей сохраняется постоянной. Поэтому, температурная зависимость проводимости полупроводника в этой области определяется температурной зависимостью подвижности носителей. Если основным механизмом рассеяния носителей в рассматриваемой области является рассеяние на тепловых колебаниях решетки, для которого характерно уменьшение подвижности с ростом температуры, то проводимость на этом участке будет падать (рис.3). Если же основным механизмом окажется рассеяние на ионизированных примесях, то подвижность, а следовательно, и проводимость в области ВС будет увеличиваться с ростом температуры. Область СD соответствует переходу к собственной проводимости. В этом случае зависимостью подвижности от температуры по сравнению с экспоненциальной зависимостью концентрации можно пренебречь, представив выражение (3) в виде
где Графиком этой зависимости является прямая, образующая угол
Резкая зависимость сопротивления полупроводников от температуры используется для устройства термосопротивлений.
|

 , (1)
, (1) - концентрация электронов и дырок в собственном полупроводнике, <ve> и <vp > - их средние скорости упорядоченного движения.
- концентрация электронов и дырок в собственном полупроводнике, <ve> и <vp > - их средние скорости упорядоченного движения. , (2)
, (2) (3)
(3) и
и  представляют собой среднюю скорость упорядоченного движения электронов и дырок при единичной напряженности электрического поля и называются подвижностью носителей.
представляют собой среднюю скорость упорядоченного движения электронов и дырок при единичной напряженности электрического поля и называются подвижностью носителей. (4)
(4) ~ T3/2 .
~ T3/2 . показан на рис.1.
показан на рис.1.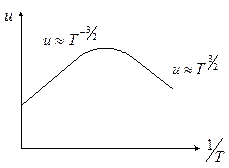 В собственных и слабо легированных полупроводниках электронный и дырочный газ является невырожденным и его концентрация весьма резко зависит от температуры. Согласно расчетам температурная зависимость концентрации носителей заряда для собственных и примесных полупроводников выражается формулами
В собственных и слабо легированных полупроводниках электронный и дырочный газ является невырожденным и его концентрация весьма резко зависит от температуры. Согласно расчетам температурная зависимость концентрации носителей заряда для собственных и примесных полупроводников выражается формулами , (5)
, (5) , (6)
, (6)

 от 1/Т представлена на рис.3.
от 1/Т представлена на рис.3. , (7)
, (7)
 . (8)
. (8) . (9)
. (9) можно определить энергию активации примесных носителей ЕD или ЕА.
можно определить энергию активации примесных носителей ЕD или ЕА. , (10)
, (10) .
. с осью абсцисс, тангенс которого пропорционален ширине запрещенной зоны
с осью абсцисс, тангенс которого пропорционален ширине запрещенной зоны . (11)
. (11)


