Определение 2.21. Векторным произведением вектора  на вектор
на вектор 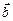 называется вектор
называется вектор  (рис. 2.15), у которого: 1) длина численно равняется площади параллелограмма, построенного на этих векторах.
(рис. 2.15), у которого: 1) длина численно равняется площади параллелограмма, построенного на этих векторах.
 2) вектор
2) вектор  перпендикулярен к плоскости, в которой лежат векторы
перпендикулярен к плоскости, в которой лежат векторы  и
и 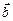 , т.е.
, т.е.  и
и  ;
;
3) вектор  направлен таким образом, чтобы кратчайший поворот от вектора
направлен таким образом, чтобы кратчайший поворот от вектора  к вектору
к вектору 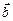 осуществлялся против часовой стрелки, если смотреть на него из конца вектора
осуществлялся против часовой стрелки, если смотреть на него из конца вектора  .
.
Векторное произведение векторов  и
и 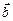 обозначается символом
обозначается символом  или
или  .
.
Из определения вытекает, что  . Свойства:
. Свойства:
1)  - антикоммутативность;
- антикоммутативность;
2)  - ассоциативность относительно скалярного множителя;
- ассоциативность относительно скалярного множителя;
3)  - дистрибутивность относительно сложения;
- дистрибутивность относительно сложения;
4) 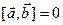 означает коллинеарность векторов
означает коллинеарность векторов  и
и 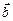 .
.
Для векторного произведения основных ортов  справедлива такая таблица (табл.2.1).
справедлива такая таблица (табл.2.1).
Таблица 2.1
С использованием этой таблицы можно доказать, что если векторы  и
и 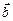 заданные своими координатами в прямоугольной системе координат
заданные своими координатами в прямоугольной системе координат 
 т.е.
т.е.
 ;
;  ,
,
то
 .
.
Если  и
и 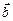 коллинеарны, то
коллинеарны, то  и из (2.31) получим, что
и из (2.31) получим, что 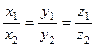 , - условие коллинеарности векторов.
, - условие коллинеарности векторов.
Векторное произведение может использоваться для вычисления площади параллелограмма, а значит, треугольника и любого плоского многоугольника, а также для вычисления момента силы. В случае, когда тело неподвижно закреплено в т. 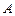 , а в т.
, а в т.  этого тела приложена сила
этого тела приложена сила  , тогда момент силы
, тогда момент силы  , а величина момента равна
, а величина момента равна  .
.
Пример Сила  приложена к точке
приложена к точке  . Определить момент этой силы относительно начала координат.
. Определить момент этой силы относительно начала координат.

 на вектор
на вектор 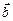 называется вектор
называется вектор  (рис. 2.15), у которого: 1) длина численно равняется площади параллелограмма, построенного на этих векторах.
(рис. 2.15), у которого: 1) длина численно равняется площади параллелограмма, построенного на этих векторах. 2) вектор
2) вектор  и
и  ;
; или
или  .
. . Свойства:
. Свойства: - антикоммутативность;
- антикоммутативность; - ассоциативность относительно скалярного множителя;
- ассоциативность относительно скалярного множителя; - дистрибутивность относительно сложения;
- дистрибутивность относительно сложения;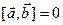 означает коллинеарность векторов
означает коллинеарность векторов  справедлива такая таблица (табл.2.1).
справедлива такая таблица (табл.2.1).



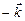


 т.е.
т.е. ;
;  ,
, .
. и из (2.31) получим, что
и из (2.31) получим, что 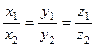 , - условие коллинеарности векторов.
, - условие коллинеарности векторов.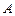 , а в т.
, а в т.  этого тела приложена сила
этого тела приложена сила  , тогда момент силы
, тогда момент силы  , а величина момента равна
, а величина момента равна  .
. приложена к точке
приложена к точке  . Определить момент этой силы относительно начала координат.
. Определить момент этой силы относительно начала координат.


