Скалярное произведение двух векторов и его свойства
Определение. Скалярным произведением двух векторов Скалярное произведение векторов Итак, по определению
где Если хотя бы один из векторов нулевой, то угол не определен и скалярное произведение по определению считают равным нулю. Поскольку по формуле
то формулу скалярного произведения можно записать еще и таким образом:
или
Таким образом, скалярное произведение двух векторов равно произведению модуля одного из векторов на проекцию второго вектора на направление первого. Скалярное произведение имеет следующие свойства: 1.Скалярное произведение коммутативно, то есть для любых векторов 2. 3. Скалярное произведение равно нулю тогда и только тогда, когда сомножители ортогональны или хотя бы один из них равен нулю. 4. Скалярное произведение ассоциативно относительно скалярного множителя, то есть 5. Скалярное произведение дистрибутивный относительно сложения, то есть для произвольных трех векторов
6. Векторы ортонормального базиса удовлетворяют соотношениям:
Рассмотрим теперь два вектора Т.е. Тогда, пользуясь перечисленными свойствами скалярного произведения, получим,
Косинус угла между двумя векторами Для ортонормального базиса получим:
и условие ортогональности двух векторов приобретает вид: Если при при
|

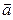 и
и 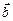 называется число, равное произведению модулей векторов
называется число, равное произведению модулей векторов  , или
, или 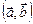 .
.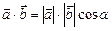 ,
, - угол между векторами
- угол между векторами 
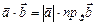
 .
.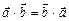 . (2.14)
. (2.14)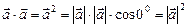 , т.е. для произвольного вектора его скалярный квадрат равняется квадрату модуля этого вектора. Отсюда
, т.е. для произвольного вектора его скалярный квадрат равняется квадрату модуля этого вектора. Отсюда 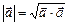 . (2.15)
. (2.15)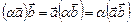 . (2.16)
. (2.16)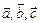 имеет место равенство
имеет место равенство .
.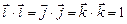 ,
,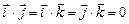 .
.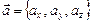 ;
;  ,
, ,
, 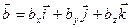 .
.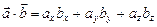 , скалярное произведение двух векторов в ортонормальном базисе равно сумме произведений их соответствующих координат.
, скалярное произведение двух векторов в ортонормальном базисе равно сумме произведений их соответствующих координат. , модуль вектора равен корню квадратному из суммы квадратов его координат.
, модуль вектора равен корню квадратному из суммы квадратов его координат. .
.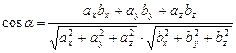
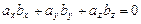 .
.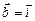 ,
, 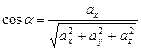 ,
,
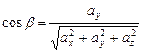 ,
,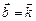
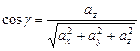 .
.


