Линейные операции над векторами. Линейными операциями над векторами называются операции сложения (вычитания) векторов и умножения вектора на число
Линейными операциями над векторами называются операции сложения (вычитания) векторов и умножения вектора на число. Рассмотрим их. Определение Произведением вектора на число называется вектор, совпадающий по направлению с вектором, если, имеющий противоположное направление, если отрицательное. Длина этого вектора равна произведению длины вектора на модуль числа.
При умножении вектора на число его координаты умножаются на это число. Действительно, если
Произведением вектора Отметим, что вектор, длина которого равна 1, называется единичным (или ортом). Пользуясь операцией умножения вектора на число, любой вектор можно выразить через единичный вектор того же направления. Действительно, поделив вектор Определение Суммой двух векторов
По определению равных векторов
Итак, для того чтобы построить вектор суммы, надо к концу первого вектора пристроить начало второго, к концу второго пристроить начало третьего и так далее. Тогда вектором суммы и будет вектор, который соединяет начало первого из векторов с концом последнего.
|

 Пример. Построить вектор
Пример. Построить вектор 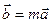 , если
, если  и
и  (рис. 2.3).
(рис. 2.3). , то
, то .
. на
на  называется вектор
называется вектор  ;
;  - противоположено направленный
- противоположено направленный 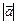 (т.е. умножив
(т.е. умножив 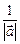 ), получим единичный вектор того же направления, что и вектор
), получим единичный вектор того же направления, что и вектор  . Отсюда следует, что
. Отсюда следует, что  .
.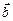 называется вектор
называется вектор  , который выходит из их общего начала и является диагональю параллелограмма, стороны которого векторы
, который выходит из их общего начала и является диагональю параллелограмма, стороны которого векторы 
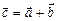 .
. поэтому
поэтому  - правило треугольника. Правило треугольника можно распространить на любое количество векторов и таким образом получить правило многоугольника:
- правило треугольника. Правило треугольника можно распространить на любое количество векторов и таким образом получить правило многоугольника:  - это вектор, который соединяет начало первого вектора
- это вектор, который соединяет начало первого вектора  (рис. 2.5).
(рис. 2.5).



