Скалярные и векторные величины
Других божеств не призывает».
Скалярные и векторные величины Из курса элементарной физики известно, что некоторые физические величины, такие как температура, объем, масса тела, плотность и т.д., определяются только числовым значением. Такие величины называются скалярными величинами, или скалярами. Для определения же некоторых других величин, таких как сила, скорость, ускорение и тому подобных, кроме числовых значений необходимо задать еще и их направление в пространстве. Величины, которые кроме абсолютной величины характеризуются еще и направлением, называются векторными. Определение Вектором называется направленный отрезок, который определяется двумя точками: первая точка определяет начало вектора, а вторая - его конец. Поэтому еще говорят, что вектор - это упорядоченная пара точек. На рисунке вектор изображается отрезком прямой, на котором стрелкой отмеченное направление от начала вектора к его концу. Например, рис. 2.1.
К векторам относится нулевой вектор, у которого начало и конец совпадают. Он обозначается Расстояние между началом и концом вектора называется его длиной, или модулем. Модуль вектора обозначается двумя вертикальными черточками слева: Векторы, параллельные до одной прямой, называются коллинеарными. Векторы, лежащие в одной плоскости или параллельные одной и той же плоскости, называются компланарными. Нулевой вектор считается коллинеарным к любому вектору. Длина его равна 0. Определение Два вектора Это записывают так: Из определения равенства векторов вытекает, что при параллельном переносе вектора получается вектор, равный начальному, потому начало вектора можно разместить в любую точку пространства. Такие векторы (в теоретической механике, геометрии), начало которых можно размещать в любой точке пространства, называют свободными. И именно такие векторы мы будем рассматривать. Определение Система векторов Определение Базисом в пространстве называются произвольные три некомпланарных вектора, которые взяты в определенной последовательности. Определение Если Координаты вектора будем писать в фигурных скобках после обозначения вектора. Так, например, Из свойств умножения вектора на число и сложения векторов вытекает утверждение относительно линейных действий над векторами, которые заданы координатами. Для того, чтобы найти координаты вектора, если известны координаты его начала и конца, необходимо из соответствующей координаты его конца отнять координату начала.
|

 Если начало вектора совпадает с точкой
Если начало вектора совпадает с точкой 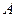 , а конец с точкой
, а конец с точкой  , то вектор обозначается
, то вектор обозначается  . Кроме этого, часто векторы обозначают одной маленькой буквой со стрелкой над ней
. Кроме этого, часто векторы обозначают одной маленькой буквой со стрелкой над ней  . В книжках иногда стрелку опускают, тогда для обозначения вектора употребляют жирный шрифт.
. В книжках иногда стрелку опускают, тогда для обозначения вектора употребляют жирный шрифт. или просто
или просто  .
. , или без стрелочек
, или без стрелочек  или
или  .
. и
и  называются равными (рис. 2.2), если они:
называются равными (рис. 2.2), если они:  1) коллинеарны; 2) сонаправлены 3) равны по длине.
1) коллинеарны; 2) сонаправлены 3) равны по длине.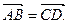 (2.1)
(2.1) называется линейно зависимой, если существуют такие постоянные
называется линейно зависимой, если существуют такие постоянные  , среди которых есть хотя бы одна отличная от нуля, и для которых выполняется равенство
, среди которых есть хотя бы одна отличная от нуля, и для которых выполняется равенство  .
.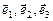 - базис и вектор
- базис и вектор  , то числа
, то числа  называются координатами вектора
называются координатами вектора  в данном базисе.
в данном базисе. означает, что вектор
означает, что вектор  .
.