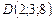По формуле (2.33)  .
.
 , так как соединяет точку
, так как соединяет точку 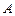 с началом координат. По условию
с началом координат. По условию  .
.
По формуле 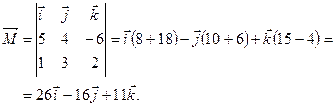
Т.о., 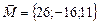 .
.
Смешанное произведение трех векторов
Определение Смешанным произведением трех векторов  и
и  называется число, полученное, если перемножить векторы
называется число, полученное, если перемножить векторы  и
и 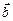 векторно, а потом полученный вектор умножить скалярно на вектор
векторно, а потом полученный вектор умножить скалярно на вектор  . Поэтому это произведение еще называется векторно-скалярным произведением. Смешанное произведение записывается таким образом:
. Поэтому это произведение еще называется векторно-скалярным произведением. Смешанное произведение записывается таким образом:  , т.е.
, т.е. 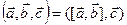 .
.
С геометрической точки зрения смешанное произведение некомпланарных векторов  и
и  по модулю равно объему параллелепипеда, построенного на векторах
по модулю равно объему параллелепипеда, построенного на векторах 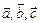 .
.
Если векторы  и
и  заданы координатами в прямоугольной системе координат
заданы координатами в прямоугольной системе координат


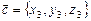
то можно показать, что  .
.
Если  , то это означает, что параллелепипед на этих векторах построить нельзя, то есть векторы
, то это означает, что параллелепипед на этих векторах построить нельзя, то есть векторы  и
и  лежат в одной плоскости, ведь
лежат в одной плоскости, ведь
 выражает условие компланарности векторов
выражает условие компланарности векторов  и
и  .
.
Смешанное произведение имеет такие свойства:
1)  - операции скалярного и векторного произведений можно менять местами, поэтому смешанное произведение записывают еще в виде
- операции скалярного и векторного произведений можно менять местами, поэтому смешанное произведение записывают еще в виде  ;
;
2) круговая перестановка множителей не изменяет величины смешанного произведения  ;
;
3) перестановка двух соседних множителей изменяет знак произведения на противоположный  .
.
Пример. Найти объем пирамиды с вершинами 
 и
и 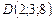

 .
. , так как соединяет точку
, так как соединяет точку 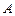 с началом координат. По условию
с началом координат. По условию  .
.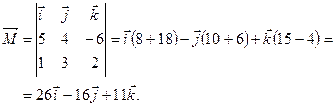
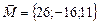 .
. и
и  называется число, полученное, если перемножить векторы
называется число, полученное, если перемножить векторы  и
и 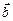 векторно, а потом полученный вектор умножить скалярно на вектор
векторно, а потом полученный вектор умножить скалярно на вектор  , т.е.
, т.е. 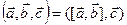 .
.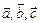 .
.

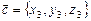
 .
. , то это означает, что параллелепипед на этих векторах построить нельзя, то есть векторы
, то это означает, что параллелепипед на этих векторах построить нельзя, то есть векторы  выражает условие компланарности векторов
выражает условие компланарности векторов  - операции скалярного и векторного произведений можно менять местами, поэтому смешанное произведение записывают еще в виде
- операции скалярного и векторного произведений можно менять местами, поэтому смешанное произведение записывают еще в виде  ;
; ;
; .
.
 и
и