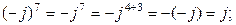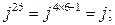Решение. 1. Алгебраическая формакомплексного числа имеет вид
1. Алгебраическая форма комплексного числа имеет вид
2. Тригонометрическая – 3. Показательная – Чтобы перейти от алгебраической к тригонометрической и показательной форме, нужно определить модуль
где Перейдем от алгебраической формы комплексного числа Сначала запишем
Изобразим комплексное число
Рис. 2. Из рисунка видно, что аргумент По формулам (2) и (3) соответственно запишем
Аналогично представим число
Рис. 3
2. Выполним действия: 1) Чтобы умножить два комплексных числа в тригонометрической форме, нужно перемножить их модули, а аргументы сложить:
2) Чтобы поделить два комплексных числа в показательной форме, нужно поделить их модули, а аргументы отнять.
3) Чтобы возвести комплексное число в
В примере учтено то, что 4) Чтобы извлечь корень
Если
Пример 2. Найти действительные числа из условия равенства двух комплексных чисел: Решение
Выделим в обеих частях равенства действительные и мнимые части:
Используя условие равенства двух комплексных чисел, составим систему: Ответ: Пример 3. Найти модуль и главные значения аргумента комплексных чисел:
а)
б)
в) г)
д)
е)
є)
Пример 4. Вычислить:
|

 , (1)
, (1)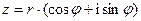 , (2)
, (2) . (3)
. (3) и аргумент
и аргумент 
 комплексного числа по формулам:
комплексного числа по формулам: , (4)
, (4) (5)
(5) - действительная часть комплексного числа,
- действительная часть комплексного числа,  - мнимая часть комплексного числа.
- мнимая часть комплексного числа. к тригонометрической и показательной форме.
к тригонометрической и показательной форме. ,
,  . По формуле (4) определим модуль комплексного числа
. По формуле (4) определим модуль комплексного числа  :
: .
.
 . Найдем значение аргумента по формуле(5). Поскольку
. Найдем значение аргумента по формуле(5). Поскольку  , то
, то  .
. ,
, .
. в тригонометрической и в показательной форме (рис. 3)
в тригонометрической и в показательной форме (рис. 3)  ,
,  .
.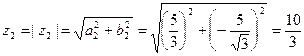 .
.
 ,
, .
. .
. в тригонометрической форме.
в тригонометрической форме.

 .
. в показательной форме.
в показательной форме.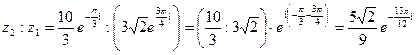 .
. в тригонометрической форме.
в тригонометрической форме. -ю степень, используется формулу Муавра
-ю степень, используется формулу Муавра  .
.
 .
. ;
;  .
.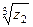 в показательной форме.
в показательной форме. , где
, где  .
. .
.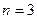 ,
,  .
. , то
, то  ;
; ; то
; то  .
.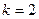 то
то  .
.
 .
.




 Решение
Решение ,
, 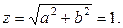
 так как вектор, изображающий комплексное число, лежит на положительной полуоси Оу;
так как вектор, изображающий комплексное число, лежит на положительной полуоси Оу;


 так как вектор, изображающий комплексное число, лежит на отрицательной полуоси Оу;
так как вектор, изображающий комплексное число, лежит на отрицательной полуоси Оу;









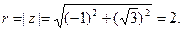

 или
или 






 .
.