Непрерывных сигналов
1. Цель работы: Изучение процессов временной дискретизации импульсных сигналов и их последующего восстановления с помощью фильтра нижних частот (ФНЧ).
2. Теоретические основы дискретизации сигналов: Как известно [1, 2] детерминированный сигнал s(t), имеющий конечное значение энергии
может быть представлен в виде весовой суммы элементарных сигналов
где
t1, t2 – моменты времени начала и окончания сигналов. Система чисел с n называется обобщенным спектром сигнала s (t) в ортогональной системе функций φn (t). При n=k в равенстве (3) интеграл равен квадрату нормы функции φn (t):
Выбирая специальным образом постоянные коэффициенты в функциях φn (t), можно добиться условия нормировки, при котором
которое является скалярным произведением функций s (t) и φn (t) [1, 2]. Равенство (5) может быть доказано подстановкой в него разложения (2) с учетом условий ортогональности (3) и нормировки (4) при Частным случаем представления (2) является тригонометрический ряд Фурье:
где
Т – интервал времени, на котором существует процесс s (t), или период сигнала s(t), если он является периодическим. Как видно из приведенных выражений, ортогональной системой базисных функций в данном случае является система тригонометрических функций:
1, cos ωt, sin ωt, cos 2ωt, sin 2ωt, … (7)
где Как указано выше, представление сигнала s (t) тригонометрическим рядом Фурье справедливо в случае существования сигнала s (t) на конечном отрезке времени длительностью Т (тогда его представление рядом (6) справедливо только для значений времени t, находящихся на этом отрезке) или для периодического сигнала с периодом T. Тогда ряд (6) справедлив для любых моментов времени. Если сигнал s (t) имеет спектральную функцию (спектральную плотность) GS(ω), отличающуюся от нуля на отрезке частот При этом выполняется равенство:
в котором
Сформулированное выше положение о возможности представления непрерывного сигнала своими отдельными (дискретными) значениями в отечественной литературе часто называется теоремой Котельникова или теоремой отсчетов. Практическое значение ее заключается в том, что для передачи через канал связи непрерывного сигнала (сообщения) s(t) с ограниченной полосой частот достаточно передавать последовательность его дискретных значений Для восстановления s(t) на приемной стороне при этом необходимо сформировать процесс
где δ;(t) – дельта-функция, и подать его на вход идеального ФНЧ с частотой среза Fв, импульсной реакцией которого является функция:
где Кф (0) – значение коэффициента передачи фильтра на нулевой частоте. Полагая Кф (0) =1/2Fв, можно получить на выходе фильтра сигнал, описываемый функцией (8), если на вход подать сигнал s1 (t), описываемый выражением (10). Однако процессы, имеющие спектральную плотность, удовлетворяющую условиям теоремы отсчетов, могут быть предсказаны на сколь угодно большой отрезок времени вперед и, следовательно, не могут нести информацию. Реальные процессы, являющиеся переносчиками информации, могут иметь, спектральную плотность, равную нулю, только в отдельных точках частотной оси. Поэтому их временная дискретизации должна сопровождаться искажением формы восстановленного процесса и, следовательно, потерями информации [2]. Можно показать, что относительная среднеквадратичная ошибка, вызываемая дискретизацией непрерывного процесса x (t), может быть найдена из выражения
где Sx (t) – спектральная плотность мощности процесса x(t); Fд=1/∆t – частота дискретизации. Как следует из равенства (12), величина среднеквадратичной ошибки, вызванной дискретизацией, определяется энергией части сигнала х (t), содержащейся в участке спектра, отброшенном предположением о верхнем значении его частоты Fв = 0,5Fд. Наряду с указанной, существуют дополнительные ошибки, которые вызваны невозможностью формирования сигнала на приемной стороне в полном соответствии с формулой (8), так как на практике невозможно сформировать импульс, подобный δ; -функции, и невозможно создать идеальный ФНЧ. Замена δ; -функции импульсом конечной амплитуды и конечной длительности, как и замена идеального ФНЧ реальным, частотная характеристика которого не имеет нулевого коэффициента передачи на отрезке частот конечной длительности, приводит к ошибкам, которые в первом приближении могут быть оценены методами, разработанными для оценки значений комбинационных искажений, возникающих при демодуляции сигналов с АИМ фильтром нижних частот.
3. Описание лабораторной установки: Лабораторная работа выполняется компьютерной модели, структурная схема которой приведена на рис 1. Она составляется из блоков пакета Simulink, оформленных в виде пользовательской библиотеки Student. Часть блоков этой библиотеки составляют специальные блоки, созданные для выполнения функций узлов радиотехнических систем: усилителей, дискретизаторов, безынерционных нелинейных элементов (моделей транзисторов и диодов), RC-цепей и т. п.
Рисунок 1 – Структурная схема модели «Теорема отсчетов»
Генератор импульсов Pulse Generator формирует периодическую последовательность положительных видеоимпульсов и радиоимпульсов со скважностью, равной двум, которую можно наблюдать на осциллографе ContSignal. Параметры генератора импульсов задаются в специальном окне, которое вызывается на экран двойным нажатием правой клавиши мыши (ПКМ) на изображении блока. Амплитуда импульсов равна 1 вольту (параметр Amplitude), длительность импульсов задаётся присваиванием параметру Period (secs) одного из трёх значений 0.2 мс, 0,4 мс или 0,8 мс, скважность – параметру Pulse Width (% of Period) значения 50. Параметр Phase delay (secs) равен 0. Аналогичным образом устанавливаются параметры несущей (генератора гармонических колебаний Sine Wave): с помощью параметра Amplitude задаётся амплитуда, равная 1 вольту, постоянная составляющая (параметр Bias) равна 0, частота несущего колебания, равная 10 кГц, задаётся как 2*pi*10e3 (параметр Frequency, rad/secs), а фаза (параметр Phase, rad) – равным pi/2 (число π записывается как pi). Параметром Phase (rad) можно менять начальную фазу несущей и пределах от 0° до 360о, задавая этот параметр также в радианах. Сформированный сигнал поступает на устройство дискретизации – блок Discretizator (рисунок 2). Частота дискретизации задается с помощью параметра Frequency digitations, Hz, и может принимать значения 10, 20, 40 и 80 кГц. Последовательность отсчетов может наблюдаться с помощью блока-осциллографа DiscrSignal. При настройке осциллографов следует сделать засечку в пункте Save data to workspace для сохранения результатов моделирования в рабочем пространстве системы MATLAB.
Рисунок 2 – Блок-схема и панель настройки подсистемы Discretizator Дискретный сигнал через переключатель Switch2 поступает на вход одного из низкочастотных фильтров Filter1 (ФНЧ1) или Filter2 (ФНЧ2) с целью восстановления непрерывного сигнала. Оба фильтра имеют частоту среза около 15 кГц, но отличаются скоростью уменьшения коэффициента передачи в области полосы затухания. Для ФНЧ1 порядок фильтра задаётся равным 4, для ФНЧ2 порядок фильтра задаётся равным 12. Амплитудно-частотные характеристики ФНЧ1 и ФНЧ2 можно определить, подключая на их входы с помощью переключателя Switch2 гармоническое колебание от генератора Sine Wave. Если же подать на входы фильтров последовательность коротких положительных импульсов с выхода блока Discretizator, то можно наблюдать импульсные реакции.
4. Домашняя подготовка к лабораторной работе: 4.1. Изучить соответствующий содержанию работы раздел курса «Радиотехнические цепи и сигналы» по учебникам, конспекту лекций и разделу 2 настоящих Указаний. 4.2. Изобразить график последовательности положительных прямоугольных импульсов длительностью 0,2мс со скважностью 2 и соответствующие ей дискретные сигналы при частоте дискретизации 10, 20, 40, и 80 кГц (в одинаковых масштабах времени). 4.3. Изобразить график последовательности радиоимпульсов длительностью 0,8 мс со скважностью 2 при частоте несущего колебания 10 кГц, а также соответствующей последовательности дискретных импульсных сигналов с указанными в п. 4.2 частотами дискретизации. 4.4. Рассчитать минимальные значении частоты дискретизации указанных п.п.4.2 и 4.3 сигналов, полагая значения верхней частоты спектра Fв равными частотам, соответствующим положению первого и второго «нулей» спектральной плотности амплитуд видеоимпульсов и первого и второго нулей после значения несущей для радиоимпульсов. Оценить погрешность дискретизации.
5. Экспериментальная часть: 5.1. Перед запуском компьютерной модели следует установить два временных параметра процесса моделирования. Для этого в команде главного меню Simulation (Моделирование) выбрать подкоманду Configuration Parameters (Параметры моделирования) и задать параметру Stop time (Конечное время) значение 0.002, а параметру Max step size (Максимальный шаг интегрирования) – значение 1e-6/10.24. 5.2. Снять АЧХ фильтров ФНЧ1 и ФНЧ2. Для этого дважды щёлкнуть мышкой по переключателю Switch2 и с выхода блока Sine Wave подать на входы фильтров гармонический сигнал амплитудой 1 В с частотой, меняющейся в пределах от 2 до 26 кГц с дискретом 2 кГц. Амплитуду выходного сигнала измерять с помощью осциллографов OutContSignal1 и OutContSignal2. Построить графики АЧХ для каждого из фильтров, определить их частоты среза и оценить степень близости их АЧХ к АЧХ идеального ФНЧ. 5.3. Исследовать импульсные реакции ФНЧ1 и ФНЧ2, подав на входы ФНЧ последовательность коротких импульсов. Для этого сначала установить оба переключателя в нижнее положение, задать для генератора Pulse Generator период (параметр Period), равный 0.8е-3 с, а частоту дискретизации в блоке Discretizator равной 2е3, т.е. 2 кГц. Зафиксировать графики импульсных реакций с экрана осциллографа в протоколе исследований, построить их в одинаковом масштабе, измерить задержку каждого из сигналов относительно момента подачи импульсов, оценить форму каждого из сигналов с точки зрении ее близости к форме импульсной реакции идеального ФНЧ. 5.4. Исследовать процесс дискретизации и восстановления видеоимпульсов длительностью 0.8 мс (параметр Period блока Pulse Generator) на частотах дискретизации 10, 20, 40 и 80 кГц (параметр Frequency digitations блока Discretizator). 5.4.1. Не изменяя структуру модели, установить длительность видеоимпульса 0.8 мс, частоту дискретизации 80 кГц и провести моделирование. Зафиксировать на выходе первого фильтра осциллограммы исходных, дискретизированных и восстановленных сигналов, а также спектры исходного и дискретизированного сигналов. Для этого либо дважды нажать на блок-кнопку GraphicsShow1 (ФНЧ1), либо перейти в командное окно системы MATLAB и запустить в нём на исполнение М-функцию обработки результатов моделирования LabRabRCS1Obr(ScopeData1). То же самое проделать для процесса на выходе второго фильтра (М-фнкция LabRabRCS1Obr(ScopeData2)). Графики (примеры графиков представлены на рисунках 3 и 4) сохранить в электронном черновике отчёта. 5.4.2. Повторить действия пункта 5.4.1 для частот дискретизации 40, 20 и 10 кГц. Все графики сохранить в электронном черновике отчёта, отмечая около них значения частоты дискретизации. 5.5. Исследовать процесс дискретизации и восстановления радиоимпульсов длительностью 0,8 мс с несущей частотой, равной 10 кГц (параметр Frequency Period блока Sine Wave). Для этого: 5.5.1. Сформировать на выходе генератора импульс длительностью 0,8 мс (параметр Period блока Pulse Generator), установить фазу гармонического колебания равной 0 (параметр Phase блока Sine Wave), перевести переключатель Switch1 в верхнее положение. Установить частоту дискретизации 40 кГц. Наблюдать на экранах осциллографов OutContSignal1 и OutContSignal2 осциллограммы исходного, дискретизированного и восстановленного сигналов. Изменяя значение параметра Phase блока Sine Wave от 0 до pi (π), проследить изменение начальной фазы радиоимпульсов, убедиться в независимости амплитуды от сдвига фазы. Графики сохранить в электронном черновике отчёта.
Рисунок 3 – Графики временных процессов, построенные с помощью М-функции LabRabRCS1Obr
Рисунок 4 – Спектры непрерывного и дискретного процессов, построенные с помощью М-функции LabRabRCS1Obr
5.5.2. Исследовать процесс дискретизации и восстановления сформированного в п. 5.5.1. непрерывного сигнала при частоте дискретизации 20 кГц (параметр Frequency Period блока Sine Wave). Наблюдать изменение формы дискретизированного сигнала от сдвига фазы несущей. Снять зависимость амплитуды и фазы восстановленного сигнала от сдвига фазы несущего колебания. Объяснить полученные зависимости. 5.5.3. Провести исследования п. 5.5.2 при частоте дискретизации 10 кГц. Объяснить полученные результаты, сформулировать рекомендации по выбору частоты дискретизации.
6. Содержание отчёта: Отчёт должен содержать: 1) цель и выполняемые в лабораторной работе задачи; 2 структурную схему лабораторной установки с подключенными внешними приборами; 3) графические зависимости и результаты расчетов, полученные в ходе домашней подготовки; 4) блок-схему Simulink-модели лабораторной установки; 5) таблицы, результаты измерений и графические зависимости, полученные в процессе экспериментальных исследований; 6) выводы по результатам работы. Выводы не должны ограничиваться перечислением выполненных исследований. Необходимо отметить основные полученные конкретные результаты, сравнить результаты расчетов и экспериментальных исследований, сформулировать рекомендации по выбору параметров устройства дискретизации и фильтров, восстанавливающих форму исходного сигнала.
7. Контрольные вопросы: 7.1. Какова практическая цель дискретизации непрерывных сигналов и сообщений? 7.2. Как оценить верхнюю частоту спектра реального сообщения или сигнала, подлежащего дискретизации? 7.3. Что такое спектр детерминированного сигнала? 7.4. Доказать ортогональность функций отсчетов. 7.5. Указать способы формирования функций отсчетов. 7.6. Сформулировать теорему отсчетов. 7.7. Пояснить с помощью спектральных диаграмм, как возникают ошибки восстановления непрерывного сигнала при использовании неидеального ФНЧ и дискретизации сигнала с неограниченной полосой частот. 7.8. Определить минимальные значения частоты дискретизации речевого сообщения и телевизионного видеосигнала. 7.9. Определить связь частоты дискретизации экспоненциального сигнала s (t) = 1(t) exp (- α t) с погрешностью его представления. Как отражается ограниченность значения Fв на форме экспоненциального сигнала после его восстановления? Лабораторная работа №2
|

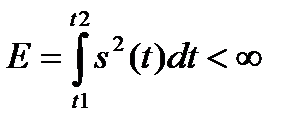 (1)
(1)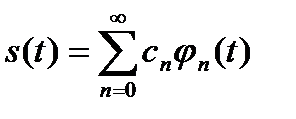 (2)
(2) – система функций, которые обладают свойством ортогональности
– система функций, которые обладают свойством ортогональности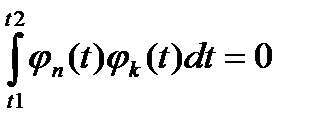 при
при  (3)
(3) . (4)
. (4) при любом n. Тогда система функций φn (t) называется ортонормированной [1, 2]. При этом спектральные коэффициенты cn могут быть найдены из выражения:
при любом n. Тогда система функций φn (t) называется ортонормированной [1, 2]. При этом спектральные коэффициенты cn могут быть найдены из выражения: (5)
(5) (6)
(6) ;
; ;
; ;
;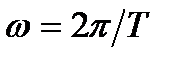 – частота первой гармоники сигнала s (t).
– частота первой гармоники сигнала s (t). , то он может быть представлен своими отдельными значениями (отсчетами), следующими через интервал времени, Δt=1/2Fв, где Fв – верхняя частота спектра s (t).
, то он может быть представлен своими отдельными значениями (отсчетами), следующими через интервал времени, Δt=1/2Fв, где Fв – верхняя частота спектра s (t). (8)
(8)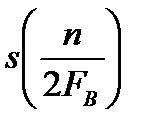 – отдельные значения (отсчеты) сигнала, играющие роль спектральных коэффициентов сn в равенствах (2) и (5), а функции образуют систему ортогональных базисных функций.
– отдельные значения (отсчеты) сигнала, играющие роль спектральных коэффициентов сn в равенствах (2) и (5), а функции образуют систему ортогональных базисных функций. (9)
(9) , следующих через интервал дискретизации
, следующих через интервал дискретизации  .
. (10)
(10) (11)
(11) (12)
(12)







