Детектирование амплитудно-модулированных сигналов
1. Цель работы: Исследование процессов детектирования амплитудно-модулированных сигналов транзисторным и диодным детекторами, а также зависимостей параметров сигналов на выходе детектора от режимов работы нелинейных элементов, на которых выполняются детекторы, от значений параметров сигналов на входе детектора и от характера нагрузки детектора. В процессе работы должны быть получены детекторные характеристики истокового детектора на полевом транзисторе и диоде, наблюдаться осциллограммы напряжений на элементах, схем детекторов.
2. Элементы теории детектирования Амплитудно-модулированных сигналов: Детектированием называется процесс выделения управляющего сигнала из модулированного. Для восстановления модулирующего процесса при обработке модулированного сигнала необходимо использовать нелинейный элемент. В частном случае детектирования амплитудно-модулированного сигнала возможно использование линейного параметрического элемента – синхронного детектора. Это следует из общего соотношения для сигнала с переменной огибающей и фазой (частотой) [1-3].
где
Как видно из приведенных выражений, огибающая E(t), фаза Ф(t) и частота ω(t) являются нелинейными функциями сигнала s(t), и для выделения содержащихся в них процессов необходимы нелинейные преобразования s(t). В случае амплитудной модуляции при постоянной фазе сигнал имеет вид:
где U0 – средняя амплитуда сигнала; λ(t) – сообщение (модулирующий процесс), нормированное таким образом, что выполняется условие М – коэффициент модуляции; ω0, φ0 – соответственно, постоянные частота несущего колебания и фазовый сдвиг сигнала. Если частота и фаза сигнала (2) известны точно, то на приемной стороне можно сформировать опорное колебание
Второе слагаемое полученного напряжения uвых (t) можно устранить фильтром нижних частот без существенных искажений для сообщения λ(t), если выполняется условие ω0 >> Ωв, где Ωв – верхняя частота спектра сообщения λ(t). Вместо процесса s0(t) на перемножитель можно подать последовательность прямоугольных импульсов со скважностью, равной двум, при условии, что её период строго равен периоду несущего колебания сигнала (2), и положение фронтов импульсов совпадает с положением «нулей» колебания Сочетание перемножителя (или коммутатора при подаче на опорный вход импульсов) с фильтром нижних частот образует синхронный детектор, который является линейным элементом с переменным коэффициентом передачи (параметрическим элементом) [2, 3]. Как видно из равенства (3), для получения достаточно высокого коэффициента передачи необходимо, чтобы фазовый сдвиг опорного колебания φ1 был близок по значению к фазовому сдвигу φ0 входного AM сигнала. Поэтому основной проблемой, которую приходится решать при построении синхронного детектора, является проблема фазировки опорного и несущего колебаний. Иными словами, при создании синхронного детектора необходимо обеспечить когерентность сигнального и опорного колебаний, что означает, в первую очередь, равенство их частот и дополнительно – близость фазовых сдвигов. Трудности создания синхронных детекторов привели к использованию для детектирования амплитудно-модулированных сигналов комбинации нелинейного элемента и фильтра нижних частот. В качестве нелинейного элемента может быть использован как транзистор, так и диод. Эффект появления низкочастотной составляющей спектра – результата нелинейного преобразования амплитудно-модулированного сигнала – можно объяснить результатом взаимодействия в нелинейном элементе (транзисторе или диоде) несущего колебания с боковыми составляющими спектра сигнала. Фильтр нижних частот выделяет низкочастотные и отсеивает высокочастотные составляющие, частоты которых близки к несущей и выше ее. Некоторые показатели качества детектора можно оценить по характеристике детектирования [2, 3], которая представляет собой зависимость приращения постоянной составляющей тока нелинейного элемента детектора от амплитуды входного высокочастотного напряжения. Выходным параметром детекторной характеристики может служить и приращение постоянной составляющей напряжения на сопротивлении нагрузки детектора. Рассмотрим аппроксимацию тока полупроводникового прибора как функцию подводимого напряжения в виде полинома третьего порядка. Как известно [2, 3], подобная аппроксимация обычно применяется при относительно небольших амплитудах переменных напряжений:
где Uc – постоянное напряжение смещения. Выделяя постоянную составляющую в составе тока, описываемого равенством (4), можно получить:
Выделяя в полученном выражении слагаемые, зависящие от амплитуды сигнала UM, получаем выражение для характеристики детектирования:
Как видно из полученного выражения, характеристика является квадратичной функцией амплитуды подводимого напряжения. При амплитудной модуляции обычно зависимость амплитуды от сообщения является линейной функцией:
где UM0 – среднее значение амплитуды; М – коэффициент модуляции. λ(t) – сообщение, нормированное к единице | λ|макс= 1. Можно убедиться, что при использовании детектора с характеристикой (6), процесс на выходе получает нелинейные искажения:
где Uд – напряжение на выходе детектора; Rн – сопротивление нагрузки детектора. Предполагается, что изменение напряжения на выходе детектора не изменяет тока электронного прибора, на котором выполнен детектор. В полученном выражении (8) нелинейные искажения сообщения λ(t) представлены последним слагаемым. Полагая
где
Из выражения (9) следует, что коэффициент нелинейных искажений пропорционален коэффициенту модуляции, и при квадратичной характеристике детектирования глубина модуляции должна быть невысокой, если нелинейные искажения важны. Для получения характеристики детектирования, близкой к линейной, используются сигналы с большой средней амплитудой. При этом справедлива кусочно-линейная аппроксимация вольтамперной характеристики электронного прибора, на котором выполняется детектирование – сток-затворной при использовании полевого транзистора или зависимости тока диода от напряжения на нём в случае диодного детектора. Рассмотрим диодный детектор, вольтамперная характеристика которого при большой амплитуде входного сигнала может быть аппроксимирована линейно-ломаной зависимостью:
(10)
где S – крутизна характеристики.
Рисунок 1 – Принципиальная схема последовательного диодного детектора Для постоянной составляющей тока диода можно записать выражение:
где
θ; – угол отсечки импульса тока; Uн – параметр кусочно-линейной аппроксимации характеристики, равный значению напряжения, начиная с которого характеристика становится линейно растущей (при S > 0), для диода можно полагать Uн = 0; Uс – напряжение смещения рабочей точки относительно u = 0. Учитывая, что в диодном детекторе напряжение на нагрузке приложено навстречу движения тока, можно полагать Uc = -Uд, где Uд – напряжение на выходе детектора, равное:
где Rн – сопротивление нагрузки детектора. Таким образом
Уравнение (15) позволяет найти угол отсечки θ;, а cos (θ;) можно назвать коэффициентом передачи детектора. При достаточно большом значении сопротивления нагрузки, когда выполняется неравенство S Rн >> 1, угол θ; является небольшим и величина cos (θ;) близка к единице. Разделив левую и правую части равенства (15) на cos (θ;), разлагая tg (θ;) в ряд Тейлора и ограничиваясь двумя членами разложения
Тогда характеристика детектирования может быть описана зависимостью
и представляет собой прямую, исходящую из начала координат с наклоном, практически равным единице. В реальных случаях начало характеристики детектирования имеет квадратичный характер из-за малых амплитуд входного сигнала и с ростом UМ парабола постепенно переходит в линейную зависимость (17). Процессы, происходящие в истоковом детекторе, выполненном на полевом транзисторе, при больших амплитудах входного сигнала подобны процессам, описанным выше, в «линейном» диодном детекторе. Упрощённая принципиальная электрическая схема истокового детектора приведена на рисунке 2.
Рисунок 2 – Упрощенная принципиальная схема истокового детектора на полевом транзисторе с «левой» характеристикой
Для получения линейной детекторной характеристики напряжение смещения в истоковом (как и в стоковом) детекторе подбирается равным начальному напряжению Uн. В общем случае угол отсечки θ в истоковом детекторе определяется выражением
Учитывая указанное выше условие Uн = Uс, можно получить выражение Для обеспечения качества выделения огибающей входного сигнала важное значение имеет выбор ёмкости нагрузки детектора. Постоянная времени нагрузки детектора должна быть намного выше периода несущей частоты сигнала и ниже периода высшей частоты спектра огибающей входного сигнала:
2π/ω0 << RнCн < 2π/Ωв (19)
Первое условие необходимо для хорошей фильтрации напряжения несущей частоты, а второе называется условием безынерционности детектора для огибающей и служит для устранения искажений огибающей, которые возможны, если при уменьшении амплитуды напряжения на входе детектора ёмкость нагрузки не успеет разрядиться и напряжение на ней «запрёт» диод.
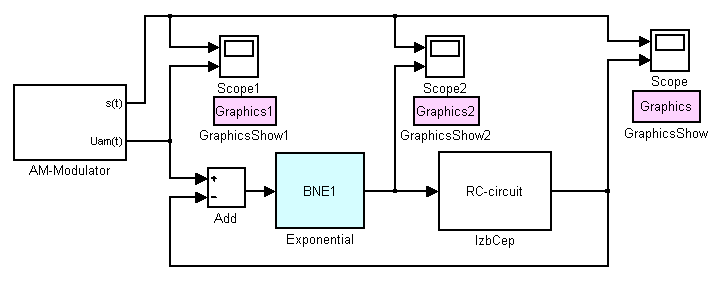
3. Характеристика лабораторной установки: Лабораторная работа №3 выполняется с помощью пакета Simulink с использованием блоков из библиотеки Student. При исследовании модели истокового детектора используется три безынерционные модель полевого транзистора, уже применявшиеся в лабораторной работе № 2. При исследовании модели последовательного диодного детектора используется также безынерционная кусочно-линейная модель диода, в качестве нагрузки которого используется RC-цепь. Генератор модулированных колебаний подключается к входу АМ-детекторов, для измерения параметров на выходе которых используется осциллограф. Кроме того, результаты моделирования передаются в рабочее пространство системы MATLAB, на основании которых М-функция LabRabRCS3Obr(simout) строит графики временных зависимостей и спектральные диаграммы процессов на выходе детекторов.
4. Домашняя подготовка к лабораторной работе: 4.1. Ознакомиться с теоретическими вопросами построения детекторов AM сигналов по литературе [1], [2], [3] и разделу 2 настоящих указаний. 4.2. Используя результаты аппроксимации сток-затворной характеристики полевого транзистора, полученные при подготовке к лабораторной работе № 2, рассчитать характеристику детектирования при полиномиальной аппроксимации для напряжений смещения Uc1, соответствующего значению тока стока Ic = 1 мА и Uc2, соответствующего току Ic = 0,1мА. 4.3. Для диодного детектора рассчитать угол отсечки θ; при крутизне характеристики диода S = 10 мА/В и сопротивлениях нагрузки Rн = 100 кОм и Rн = 30 кОм, определить коэффициент передачи детектора. 4.4. Определить допустимые значения емкости нагрузки при f0= 200 кГц, частоте модуляции F = 1 кГци сопротивлении нагрузки Rн= 30 кОм. 4.5. Ответить на контрольные вопросы п. 7 настоящих указаний.
5. Порядок выполнения лабораторной работы: 5.1. Собрать блок-схему модели истокового детектора (рисунок 3), используя блоки пользовательской библиотеки Student. Установить необходимые параметры АМ-модулятора, безынерционного блока модели транзистора, параметры RC-цепи нагрузки и фильтра нижних частот.
Рисунок 3 – Структурная схема модели истокового детектора
- блок AM-Modulator – Ao = 1; f0 = 2*pi*200e3; M = 0.5; F = 2*pi*1e3; - блок Analog Filter Design – Design Method = Butterworth; Filter type = Lowpass; Filter order = 8; Passband edge frequency = 2*pi*15e3; Параметры блоков модели полевого транзистора устанавливаются по результатам расчёта домашнего задания. Блок BNE1 по умолчанию имеет значения параметров: Io = 1e-9; mfi = 0.026; R = 0.5. Параметры моделирования установить следующими: – конечное время Stop time = 1e-2; – шаг интегрирования Fixed step size = 8e-3/2^14 (фиксированная величина шага решателя). 5.2. Снять статическую детекторную характеристику – зависимость приращения постоянного напряжения на истоке транзистора от амплитуды высокочастотного напряжения на входе детектора (на затворе транзистора) при использованных в домашней подготовке напряжениях смещения. Для этого выбрать кусочно-линейную модель ВАХ транзистора, установив переключатели Sw1 и Sw2 в соответствующие положения. В блоке AM-modulator менять амплитуду высокочастотного напряжения Ао в пределах от 0 до 5 В с детальными измерениями на участке изменения амплитуды от 0 В до 1 В. Величину постоянного напряжения, снимаемого с выхода аналогового НЧ-фильтра, измерять с помощью осциллографа Signal, причём область измерения выбирать на установившемся участке осциллограммы. Здесь и далее фиксировать осциллограммы напряжений на элементах детектора с помощью блока GraphicsShow или пользовательской М-функции LabRabRCS3Obr. 5.3. Снять при тех же значениях параметров динамическую детекторную характеристику истокового детектора – зависимость амплитуды U н НЧ-сигнала на выходе детектора от коэффициента модуляции М. Для этого амплитуду несущей U М установить равной 5 В, частоту модуляции 1 кГц. По формуле
определить зависимость коэффициента передачи истокового детектора. Построить график зависимости K ИД(М) и показать его преподавателю. 5.4. Повторить измерения пунктов 5.2 и 5.3, подключив к выходу кусочно-линейной модели транзистора вместо аналогового фильтра другую избирательную цепь – RC -цепь (переключатель Sw3). Сопротивление нагрузки R выбрать равным 30 кОм, ёмкость конденсатора 20 нФ. Амплитуду напряжения на входе детектора менять в тех же пределах. Проделать эти же измерения при сопротивлениях нагрузки 15 кОм и 60 кОм. 5.5. Собрать блок-схему модели диодного детектора (рисунок 4), заменив в блок-схеме на рисунке 4 блоки модели транзистора и RC -цепи блоками из пользовательской библиотеки Student. Установить параметры модели реального диода и параметры RC -цепи детектора.
Рисунок 4 – Блок-схема моделирования диодного детектора
5.6. Снять статическую детекторную характеристику диодного детектора – зависимость постоянного напряжения на выходе RC -цепи от амплитуды высокочастотного напряжения Ао в пределах от 0 до 5 В с детальными измерениями на участке изменения амплитуды от 0 В до 1 В. Зафиксировать с помощью блоков GraphicsShow осциллограммы напряжений на элементах диодного детектора при различных значениях ёмкости нагрузки – малой (5 нФ), оптимальной (20 нФ) и избыточной (80 нФ). 5.7. Снять динамическую детекторную характеристику диодного детектора – зависимость амплитуды U н НЧ-сигнала на выходе детектора от коэффициента модуляции М при оптимальном значении ёмкости RC -цепи. Для этого амплитуду несущей U М установить равной 5 В, частоту модуляции 1 кГц. По формуле (20) определить зависимость коэффициента передачи диодного детектора K ДД(М). Построить график зависимости K ДД(М) и показать его преподавателю.
6. Содержание отчёта: Отчёт по лабораторной работе должен содержать: 1) цель и решаемые в лабораторной работе задачи; 2) блок-схему установки с подключенными приборами; 3) результаты домашних расчётов; 4) изображения блок-схем Simulink-моделей истокового детектора и диодного детектора; 5) осциллограммы напряжений в различных точках схем детекторов, согласованные во времени с соблюдением масштаба по напряже нию и построенные с помощью пользовательской М-функции LabRabRCS3Obr(simout) (рисунок 5);
Рисунок 5 – Временные и спектральные диаграммы при моделировании истокового детектора
7. Контрольные вопросы: 7.1. Назовите условия, при которых наблюдается квадратичное и при которых наблюдается линейное детектирование. 7.2. В чем преимущества и недостатки линейного детектора по сравнению с квадратичным? 7.3. Привести принципиальную схему диодного детектора и указать назначение элементов. 7.4. Пояснить принцип действия истокового детектора и изобразить его схему. Указать достоинства и недостатки первого по отношению ко второму. 7.5. Какими соображениями следует руководствоваться при выборе элементов нагрузки диодного детектора? 7.6. Как будет изменяться угол отсечки при уменьшении сопротивления нагрузки? 7.7. Изобразить форму напряжения на выходе диодного детектора при отключенной емкости нагрузки. 7.8. Что такое статическая детекторная характеристика? Каким образом она измеряется? 7.9. Что такое динамическая детекторная характеристика? Каким образом она измеряется? 7.10. Указать причины, которые могут вызвать нелинейные искажения напряжения на выходе детектора. 7.11. В чём преимущества и недостатки синхронного амплитудного детектора по сравнению с диодным? 7.12. Изобразить структурную схему модели диодного детектора и пояснить на ней работу узлов реального диодного детектора.
|

 (1)
(1) – огибающая сигнала;
– огибающая сигнала; – полная фаза сигнала;
– полная фаза сигнала; – мгновенная частота сигнала;
– мгновенная частота сигнала;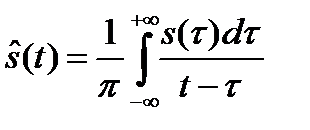 – процесс, сопряженный по Гильберту с сигналом s(t) (прямое преобразование Гильберта по отношению к сигналу s(t)),
– процесс, сопряженный по Гильберту с сигналом s(t) (прямое преобразование Гильберта по отношению к сигналу s(t)),  ,
,  .
. (2)
(2)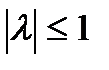 ;
; и подать его на перемножитель вместе с сигналом s(t). Тогда после умножения можно получить:
и подать его на перемножитель вместе с сигналом s(t). Тогда после умножения можно получить: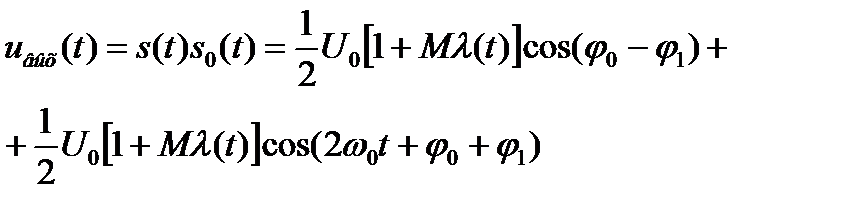 (3)
(3) . Необходимость в фильтре нижних частот сохраняется и в этом случае.
. Необходимость в фильтре нижних частот сохраняется и в этом случае. (4)
(4)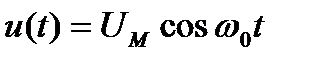 – переменное входное напряжение с амплитудой UM и частотой ω0;
– переменное входное напряжение с амплитудой UM и частотой ω0;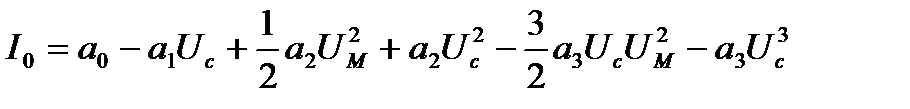 (5)
(5) (6)
(6) (7)
(7) (8)
(8) , можно оценить коэффициент нелинейных искажений Кν как отношение амплитуды второй гармоники косинусоидального закона изменения сообщения к амплитуде его первой гармоники.
, можно оценить коэффициент нелинейных искажений Кν как отношение амплитуды второй гармоники косинусоидального закона изменения сообщения к амплитуде его первой гармоники. (9)
(9) – амплитуда второй гармоники сообщения;
– амплитуда второй гармоники сообщения; – амплитуда первой гармоники сообщения λ(t).
– амплитуда первой гармоники сообщения λ(t). (11)
(11) – коэффициент разложения косинусоидального импульса для постоянной составляющей:
– коэффициент разложения косинусоидального импульса для постоянной составляющей: (12)
(12) (13)
(13) (14)
(14) (15)
(15) , можно получить приближенное равенство:
, можно получить приближенное равенство: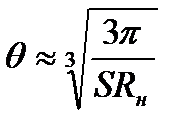 (16)
(16) (17)
(17)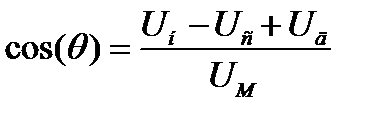 (18)
(18) , аналогичное подобному выражению в диодном детекторе. Поэтому детекторная характеристика истокового детектора при больших значениях амплитуды входного сигнала также является линейной.
, аналогичное подобному выражению в диодном детекторе. Поэтому детекторная характеристика истокового детектора при больших значениях амплитуды входного сигнала также является линейной.
 (20)
(20)