Гидростатика

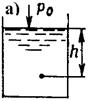
Гидростатика изучает законы равновесия жидкой среды и взаимодействие жидкости с твердыми телами, т.е. в ситуациях, когда движение отсутствует или скорость пренебрежительно мала.

Гидростатика позволяет понять некоторые свойства такой важной гидродинамической величины, как давление. Давление твердого тела определяется его весом, давление жидкости - ее глубиной. Сила давления на дно сосуда р (рис.1,а) не зависит от его формы, а определяется только уровнем налитой в сосуд жидкости в соответствии с гидростатической формулой:

р = р₀ + ρgh;

р = р₀ + р_м ,

где ρ - плотность жидкости, р₀ - давление жидкости на некотором фиксированном уровне (при наличии свободной поверхности - атмосферное давление), h - отстояние по вертикали от этого уровня до рассматриваемой точки (глубина погружения), р_и - избыточное (манометрическое) давление.

Соприкасаясь с твердым телом, жидкость оказывает на него давление, направленное по нормали к поверхности тела. Сила избыточного давления жидкости на плоскую поверхность, имеющую вертикальную ось симметрии (рис.1,б)

F = ρgh_cS,

где h_c - отстояние по вертикали ц.т. площади поверхности от уровня свободной поверхности жидкости; S - площадь поверхности.

 

Рис.1. Гидростатическое давление и сила давления жидкости.

 

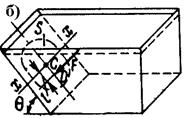
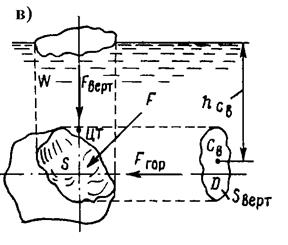
Точка D приложения равнодействующей сил давления на поверхность называемая центром давления (ц.д.), отстоит от ц.т. площади (C) на расстоянии l.

Силу избыточного давления на криволинейную поверхность (рис.1,в) определяют ее составляющие F_x, F_y и F_z, по осям координат

F = .

Горизонтальная составляющая силы давления на криволинейную поверхность (F_x или F_y)

F_гор = ρgh_cвS_верт,

где h_cв - отстояние по вертикали ц.т вертикальной проекции от плоскости гидростатического напора (рис. 1,в).

Линия действия силы F_гор проходит через центр давления D площади вертикальной проекции S_верт.

Вертикальная составляющая силы давления на криволинейную поверхность, равна весу цилиндра жидкости, ограниченного снизу поверхностью, а сверху плоскостью гидростатического напора (рис.2,а) проходит через ц.т. объема

F_верт = ρgW.

Призма над криволинейной поверхностью называется телом давления.

Объем тела давления W не обязательно совпадает с действительным объемом сосуда. Если жидкость находится под криволинейной поверхностью, объем тела давления определяется объемом над поверхностью до плоскости гидростатического напора, а сила направлена вертикально вверх (рис.2,б).

 

 

Рис.2. Силы давления на криволинейные поверхности.

 

Когда тело плавает на поверхности жидкости, объем тела давления равен объему вытесненной им воды V, т.е. объемному водоизмещению (рис.2 в,г)

F = ρgV.

Когда тело полностью погружено в жидкость, объем тела давления верхней половины его поверхности равен W_в, а нижней -W_н.

Вертикальную составляющую в таких случаях называют силой выталкивания (для плавающих тел - сила поддержания или плавучести)

F = ρg(W_н – W_в) = ρgV.

В результате получаем закон Архимеда: на погруженное в воду тело действует сила, равная весу вытесненной им воды, и направленная по вертикали вверх. Линия действия этой силы проходит через центр тяжести вытесненного объема V.

Закон Архимеда в обычной форме не применим к телам имеющие контактные со стенками сосуда поверхности, между которыми не может проникнуть жидкость. Такое тело испытывает со стороны жидкости только усилие ρgW, прижимающее его к грунту (рис.2,д). Но как только на контактную поверхность просочится жидкость, появится выталкивающая тело сила.
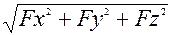